Deze samenvatting is gebaseerd op het studiejaar 2013-2014.
Het doel van dit oefenpakket is om zoveel mogelijk tentamen stof te kunnen oefenen. De opgaven zijn dan ook op tentamen niveau. Dit betekent dat ze lastig, tot zeer lastig zijn als je de reguliere stof nog niet hebt bestudeerd. Er wordt daarom ook sterk aangeraden eerst de theorie goed door te lezen voordat je deze opgaven maakt. Bij alle opgaven wordt een uitgebreide uitwerking gegeven. Tevens zal de achterliggende theorie beschreven worden, hierdoor kan je de uitkomsten makkelijker plaatsen en zal je waarschijnlijk op het tentamen beter kunnen redeneren.
Soms staat er een blok met tekst tussen de antwoorden, in dit geval gaat het om de theorie achter de opgave. Er wordt aangeraden de opgaven op volgorde af te werken; theorie die bij de eerste opgave wordt uitgelegd in de uitwerking en bij de tweede opgaven weer terug komt, wordt niet opnieuw uitgelegd in de uitwerkingen van de tweede opgave. Daarnaast staat naast elke opgave welk ‘onderwerp’ het bevat. Mocht je zwak zijn in een bepaald onderwerp dan is het aan te raden om deze opgaven nog een keer te oefenen.
De opgaven in dit oefenopgavenboek zijn in Engels. De uitwerkingen in het Nederlands. Op het tentamen krijg je waarschijnlijk ook een Engelse versie, maar mag je de antwoorden ook in het Nederlands beschrijven.
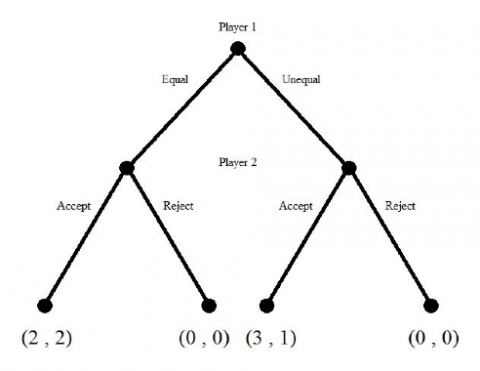
Two individuals have to agree on how to divide 4 Euros. Two divisions are being considered:
- An even split that would give 2 Euros to each of them, and
- An asymmetric division that would leave 3 Euros with one of the players, let us call him player 1, and one Euro with the other, player 2.
The following allocation procedure is considered. First, player 1 has to make a proposal, i.e., one of the previous two possibilities, to which player 2 has to respond with acceptance or rejection. If the proposal is accepted the 4 Euros are divided accordingly, whereas in the alternative case neither of them receives any money at all.
- Formulate the situation as a game, draw the game tree, and discuss informally the likelihood of different outcomes.
- Define players’ strategies, draw the normal form game, and check whether players have strictly dominant or dominated strategies. Can you solve this game by IESDS? Is this game DS?
- Find all pure strategy NE and NE outcomes. Discuss the likelihood of different NE outcomes.
Antwoord
1. Formulate the situation as a game, draw the game tree, and discuss informally the likelihood of different outcomes.
Voordat deze opgaven gemaakt worden moet eerst de intuïtie gevolgd worden. Het is een simultaan spel waarbij speler 1 eerst een voorstel doet wat speler twee vervolgens kan aannemen of verwerpen. Het zou eerlijk zijn van speler 1 om het evenredig te verdelen; ieder krijgt dan 2 euro. Maar in speltheorie moet je (helaas) niet uitgaan van het altruïsme van de mens. In dit geval wordt er dus vanuit gegaan dat speler 1 zijn ‘winst’ wil maximaliseren. Dit kan hij doet door optie twee aan te bieden. Hij krijgt dan 3 euro, zijn medespeler 1 euro. Zal speler 2 dit accepteren? Waarschijnlijk wel, want 1 euro is nog altijd meer dan geen euro’s.
De volgende allocatie procedure wordt voorgesteld:
1. Speler 1 maakt een voorstel (een van de twee mogelijkheden)
2. Speler 2 reageert door dit te accepteren of te weigeren
3. Als het voorstel wordt geaccepteerd, dan worden de 4 euro’s verdeeld zoals speler 1 dit heeft voorgesteld. In het alternatieve geval krijgt geen van beiden geld.
Het tekenen van een boomdiagram. Dit is redelijk intuïtief. Je begint bovenaan met de speler die als eerste een keuze mag maken. In dit geval speler 1. Vervolgens krijg je de keuze van speler 2, dit is te zien aan de ‘dots’. De keuzes worden weergegeven door pijlen of strepen. Een pijl kan leiden tot 1 ‘dot’, er kunnen dus niet twee pijlen naar een dot gaan. Het spel eindigt in de ‘terminale dots’, dit is een uitkomst met de corresponderende uitbetaling voor elke speler. In dit geval is het eerste getal achter de komma de uitbetaling voor speler 1, en het tweede getal de uitbetaling voor speler 2). Let er altijd bij het tekenen van een boomdiagram op dat je geen loops maakt. Dit betekent dat een keuze nooit terug kan gaan naar een keuze die al gemaakt is.
2. Define players’ strategies, draw the normal form game, and check whether players have strictly dominant or dominated strategies. Can you solve this game by IESDS? Is this game DS?
Het formuleren van de strategieën van de spelers gaat als volgt:
- Speler 1: ‘Equal’, ‘Unequal’
- Speler 2: Deze heeft twee informatie sets (‘Equal’, ‘Unequal’) met twee mogelijke acties in elke set. Deze speler heeft dus in totaal vier strategieën: AA, AR, RA and RR.
Het weergeven van het spel in ‘normale vorm’ is het weergeven van het spel in de vorm zoals je gewend bent van speltheorie, namelijk de matrix vorm. Hierin staat links vaak speler 1 en boven speler 2. Daarnaast is de uitbetaling voor de komma voor speler 1 en de uitbetaling na de komma voor speler 2.
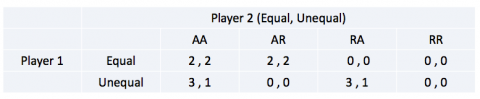
In dit geval zie je ook duidelijk de hoeveelheid strategieën van de verschillende spelers.
Heeft dit spel strikte gedomineerde of strik dominante strategieën? Even terug naar de theorie:
Een strikt dominante strategie is een strategie die altijd door de desbetreffende speler zal worden gespeeld, ongeacht wat zijn tegenstander doet. Hij zal deze strategie dan ook altijd spelen. Er kan slechts 1 strikt dominante strategie zijn per speler.
Een strikt gedomineerde strategie is een strategie die strikt wordt gedomineerd door tenminste 1 andere strategie van dezelfde speler. Het is dus nooit waardevol om deze strategie te spelen, omdat de desbetreffende speler het beter kan doen door een andere strategie te spelen. Let op! Een strategie die de strikt gedomineerde strategie domineert is niet per definitie een strikt dominante strategie.
Is er in dit geval een strikte gedomineerde strategie?
Ja, als wordt gekeken naar speler 2 heeft deze de optie uit vier strategieën. (R,R) lijkt in dit geval de minste goede strategie, er zijn namelijk alleen maar uitbetalingen van 0. Is deze dan gedomineerd? Er moet gekekn worden of er dus een andere strategie is voor speler 2 die altijd beter is om te speler dan strategie (R,R). En ja, deze is er. (A,A) is in alle opzichten beter. Dus (R,R) wordt strikt gedomineerd door (A,A). (R,R) wordt niet strikt gedomineerd door (A,R) en (R,A) want de uitbetaling (0,0) is hetzelfde, dus niet per definitie beter.
Is er in dit geval een strikt dominante strategie?
Nee, als er wordt gekeken naar de potentiële kandidaat, (A,A) zie je dat de uitbetalingen van (A,A) en (A,R) gelijk zijn in het geval dat speler 1 voor ‘Equal’ kiest. Hieruit kan worden geconcludeerd dat (A,A) niet in alle gevallen beter is, maar soms ook even goed. En dat is niet de voorwaarde voor strikte dominantie.
Hoe zit het dan met zwak gedomineerde en dominante strategieën? Weer even terug naar de theorie:
Een zwak dominante strategie is een strategie die evengoed of beter is dan alle andere strategieën van de desbetreffende speler.
Een zwak gedomineerde strategie is dus een strategie waar andere strategieën ten minste beter of gelijk zijn aan deze strategie.
Zijn er in dit geval zwak gedomineerde strategieën?
Ja. zowel (A,R) als (R,A) worden zwak gedomineerd door (A,A). In dit geval is (A,A) altijd beter of tenminste gelijk in uitbetalingen aan de andere strategieën.
We kunnen nu de zes strategieën (R,R), (R,A) en (A,R) van speler 2 elimineren.
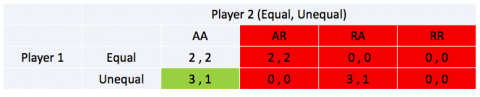
Nu wordt er gekeken naar speler 1. Gegeven dat speler 2 voor (A,A) gaat (want de rest is strikt of zwak gedomineerd door (A,A), heeft speler 1 natuurlijk twee keuzes: ‘Equal’ of ‘Unequal’. De uitbetaling van ‘Unequal’ (3) als strikt beter dan de uitbetaling van ‘Equeal’ (2). Oftewel, ook speler 1 heeft een strikt dominante strategie; ‘Unequal’.
Hoe kunnen we het spel oplossen door middel van IESDS?
IESDS is het elimineren van alle strikt gedomineerde strategieën (‘Iterative Elimination of Strictly Dominated Strategies’). De volgorde van het elimineren maakt niet uit; het antwoord zou moeten komen uit de strategie die overblijft. Let op, ook al volg je niet deze methode van IESDS, het is altijd nodig om de strikt gedomineerde strategieën te elimineren. Een strikt gedomineerde strategie kan dus nooit het antwoord van het spel zijn.
In dit geval kan de matrix niet opgelost worden door middel van IESDS, aangezien er maar 1 gedomineerde strategie kan worden geëlimineerd, namelijk (R,R).
Hoe kan het spel opgelost worden door middel van DS?
Het concept van ‘dominance solvable’ (DS) probeert het spel op te lossen door middel van het elimineren van alle zwak gedomineerde strategieën. Dit op twee voorwaarden:
- Alle zwak gedomineerde strategieën van alle spelers moeten worden geëlimineerd
- Als je dit gedaan hebt, dan moet het antwoord van alle overige vakjes (oftewel, de vakjes die niet geëlimineerd zijn) identiek zijn voor alle spelers.
Is dit spel DS? Als we alle zwak gedomineerde strategieën elimineren (zie de matrix hierboven) dan komen we uit op de strategie (‘Unequal’, AA). Is dit DS? Nee helaas, aangezien de uitbetaling van (3,1) niet identiek is. Dit betekent dat bij een DS spel allebei de spelers dezelfde uitebetaling moeten hebben.
3. Find all pure strategy Nash equilibrium and outcomes. Discuss the likelihood of different NE outcomes.
Een Nash-evenwicht (NE) is een evenwicht waar geen enkele speler van wil afwijken. Een Nash-evenwicht is dus de ‘beste reactie’ gegeven de tegenstander zijn strategie. Hoe vind je dit? Door de ‘streepjes methode’. Je zet onder elke ‘beste reactie’ van een speler een streepje.
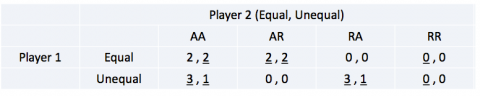
In ons geval is zijn er dus drie Nash-evenwichten:
(‘Unequal’, AA)
(‘Equal’, AR)
(‘Unequal’, RA)
De vraag die nu misschien in je opkomt, is hoe er meerdere evenwichten kunnen zijn. Dit kan in het geval van een Nash-evenwicht, echter, tot welk evenwicht het uiteindelijk zal komen is niet duidelijk uit dit spel. Hoe de spelers ertoe komen een bepaald Nash-evenwicht te spelen is een andere vraag, hierop wordt verderop op teruggekomen.
There are two movie theaters. They agree to charge $9 per ticket to maximize joint profit. However, each theater must consider whether to cheat on the agreement and offer a "2-for-1" ticket price to its customers. Consider the payoff matrix depicting their payoffs in a game played once. The payoffs are (profit to Movie Theater Y, profit to Movie Theater X).
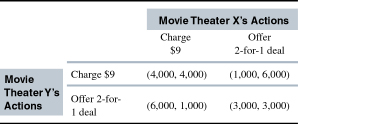
- Determine if either theater has a dominant strategy. Solve for the Nash equilibrium of the game.
- Is this game a Prisoner's Dilemma? Why, or why not?
Antwoord
De matrix laat zien dat het voor elk bedrijf lucratief is om af te wijken van het evenwicht (ze verhogen hun uitbetaling van 4000 naar 6000).
1. Determine if either theater has a dominant strategy. Solve for the Nash equilibrium of the game.
Stel dat speler Y Charge speelt, dan is het voor speler X altijd zinvol om af te wijken en 2-for-1 deal te spelen (het verhoogt zijn uitbetaling van 4000 naar 6000). Ook als speler Y 2-for-1 speelt is het voor speler X beter om af te wijken (het verhoogt zijn uitbetaling van 1000 naar 3000). Kortom, het is altijd beter om af te wijken van de actie Charge. Daarom is de strategie 2-for-1 deal altijd dominant. Als we streepjes zetten dan komen we uit op een Nash-evenwicht van (3000, 3000).
2. Is this game a Prisoner's Dilemma? Why, or why not?
Ja, dit is een typisch geval van een ‘prisoner’s dilemma’ aangezien beiden spelers slechter af zijn in het Nash-evenwicht dan dat ze ‘samenwerken’ en beiden een prijs vragen van 9.
Consider the extensive form of the sequential entry game played once. (See figure below.) The incumbent (I) has threatened to fight entry if the entrant (E) decides to enter.
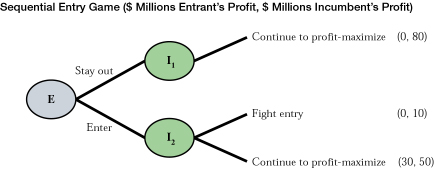
- What is the Nash equilibrium of the game? Explain.
- Is the incumbent's threat to fight entry credible? Explain.
Antwoord
In dit geval gaat het om het wel of niet aanvechten van een nieuwe binnenkomer in een voorgaande monopolie markt.
- What is the Nash equilibrium of the game? Explain.
In dit geval kan het NE opgelost worden door ‘backward inductie’. Het van achter naar voren oplossen van een boomdiagram. Er wordt dus eerst gekeken naar de ‘Incumbent’ (I). Voor hem is het meest lucratief om geen binnenkomer te hebben, maar mocht de bedrijf toch de markt betreden dan zal (I) de strategie ‘continue to profit-maximize’ kiezen (uitbetaling van 50 > 10).
Dit is bekend bij de ‘Entrant’ (E). Hij kan dus zijn winst maximaliseren door te kiezen om de markt wel te betreden aangezien het weet dat de ‘Incumbent’ (I) niet voor ‘fight’ zal kiezen. Kortom de ‘Entrant’ (E) zal de markt betreden en de ‘Incumbent’ (I) zal dit niet aanvechten. Dit is dan ook het Nash-evenwicht (30, 50).
- Is the incumbent's threat to fight entry credible? Explain.
Nee, aangezien de ‘Entrant’ (E) weet dat de ‘Incumbent’ (I) nooit het gevecht aan zal gaan aangezien dit de uitbetaling voor de ‘Incumbent’ (I) verlaagt. Echter, let hierbij op dat als dit spel vaker wordt gepeeld (herhaalde spellen) dat de dreiging wel zeker geloofwaardig kan zijn. Dan kan de ‘Incumbent’ (I) namelijk voor de strategie kiezen om de ‘Entrant’ (E) aan te vechten om zijn toekomstige monopolie winsten veilig te stellen.
Consider the actions of Coke and Pepsi to either offer a low price or advertise heavily. The payoff matrix associated with their choice of actions is shown below. Payoffs are (profit to Coke, profit to Pepsi).
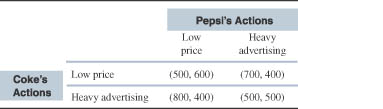
- Does either firm have a dominant strategy? If so, to do what?
- Solve for the Nash equilibrium of the game.
1. Does either firm have a dominant strategy? If so, to do what?
Geen van beiden bedrijven heeft een dominante strategie. Om dit spel op te lossen moet er ook gekeken worden naar gemixte strategieën. θ is de kans dat Coke (speler 1) voor strategie ‘low price’ kiest – de kans 1 – θ is dan de kans dat Coke voor strategie ‘heavy advertising’ kiest. P is de kans dat Pepsi ‘low price’ kiest. 1- p is de kans dat pepsie ‘heavy advertising’ kiest.
De uitbetaling voor Coke is als volgt:
[ θ (500p + 700(1-p)) ] + [ (1-θ)(800p + 500(1-p)) ]
De uitbetaling voor Pepsi is als volgt:
[ p (600θ + 400(1-θ)) ] + [ (1-p)(400θ + 500(1-θ)) ]
2. Solve for the Nash equilibrium of the game.
Dit spel heeft geen puur Nash-evenwicht. Nu moet er worden gekeken naar de gemixte strategische Nash-evenwichten.
Om een gemixte strategie te voeren moet de opbrengst van pepsi’s ‘low price’, gegeven de strategie van Coke, gelijk zijn aan die van ‘heavy advertising’ (anders zou pepsi wel voor de strategie gaan die het meeste opbrengt). Het feit dat dit bekend is verteld veel over de vergelijking die opgelost moet worden. De volgende vergelijking geeft aan waarin de kansen worden bepaald door de strategie van Coke.
600θ + 400(1 – θ) = 400θ + 500(1 – θ)
600θ + 400 – 400θ = 400θ + 500 – 500θ
300θ = 100
θ = 1/3
(1 – θ) = 2/3
Ditzelfde kan gedaan worden voor Coke. In dit geval kan gesteld worden dat Coke een strategie neemt waarin zijn opbrengsten tussen ‘low price’ en ‘heavy advertising’ gelijk zijn:
500ρ + 700(1 – ρ) = 800ρ + 500(1 – ρ)
500ρ + 700 – 700ρ = 800ρ + 500 – 500ρ
200 = 500ρ
2/5 = ρ
In dit geval is er dus sprake van een gemixt Nash-evenwicht:
(1/3, 2/3 , 2/5,3/5)
Consider the matrix (below) of two firms competing for local sales of motorboats. They've each developed two strategies—advertise big and give stuff away—to help increase sales. Payoffs are in terms of (Firm A's percentage of sales, Firm B's percentage of sales).

- Does either firm have a dominant strategy? If so, what is it?
- Solve for the Nash equilibrium of the game.
Antwoord
- Does either firm have a dominant strategy? If so, what is it?
Beiden bedrijven hebben een dominante strategie. Bedrijf A kan het beste ‘advertise big’ spelen gezien de uitbetaling (60>50 en 45>40). Bedrijf B kan het beste ‘give stuff away’ spelen gezien de uitbetaling (55>40 en 60>50).
- Solve for the Nash equilibrium of the game.
Het Nash-evenwicht in dit geval is simpel. Bedrijf A zal voor ‘advertise big’ gaan en bedrijf B zal ‘give stuff away’ spelen (45, 55)
Consider the matrix (below) of two local grocery stores in a small town. They've each developed two strategies—offer double coupons or stay open 24 hours—to help increase sales. Payoffs are in terms of (Firm A's percentage of sales, Firm B's percentage of sales).

- Does either firm have a dominant strategy? If so, what is it?
- Solve for the Nash equilibrium of the game.
Antwoord
- Does either firm have a dominant strategy? If so, what is it?
Beiden bedrijven hebben een dominante strategie. Bedrijf A kan het beste ‘stay open 24 ours’ spelen gezien de uitbetaling (45>40 en 60>55). Bedrijf B kan het beste ‘double coupons’ spelen gezien de uitbetaling (60>45 en 55>40).
George and Henry sell wool sweaters during the winter, in front of the student union of a remote college in upstate Minnesota. Because their sweaters are similar, they've developed the tactics (shown in the matrix below) to increase their sales. Payoffs are (percentage of sales to George, percentage of sales to Henry).
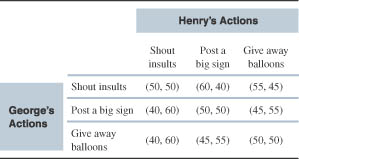
1. Does George have a dominant strategy? To do what?
2. Does Henry have a dominant strategy? To do what?
3. Solve for the Nash equilibrium of the game.
Antwoord
- Does George have a dominant strategy? To do what?
Ja, ‘shout insults’ is dominant.
- Does Henry have a dominant strategy? To do what?
Ja, opnieuw ‘shout insults’ is dominant
- Solve for the Nash equilibrium of the game.
Logischer wijs kan de rest van de strategieën elimineren; alleen de dominante strategieën blijven over. Het Nash-evenwicht is dus (shout insults, shout insults).
Stacey and Betsy are contestants on a game show. They each select a wrapped box from four choices. They know one box contains $100, one contains $1,000, one contains $10,000, and one contains $100,000. They unwrap their chosen boxes and look inside. They then have a choice of whether to trade with each other. Stacey uses all the information in the game correctly. Betsy's husband has advised her to trade if she has the box with anything less than $100,000 inside. Betsy's box has $1,000 inside. She offers to trade with Stacey. Stacey agrees to trade.
- Did Betsy's husband give her good advice?
- What was in Stacey's box? Explain.
Antwoord
De informatie die gegeven wordt op een rijtje:
- In de boxen zitten 100, 1.000, 10.000, of 100.000
- Ze mogen een box kiezen, kijken en vervolgens kiezen om te ruilen
- B heeft 1.000 in haar box.
- Ze besluit dat ze wil ruilen
- S vindt dit ok, en ruilt met B.
- Did Betsy's husband give her good advice?
In dit geval zeker niet. S zou de informatie die het spel geeft moeten meenemen in haar beslissing om te ruilen. Er zijn 4 dozen. B heeft 1.000. Ze weet niet wat S heeft, maar ze weet dat het 100, 10.000 of 100.000 is. Bedenk nu dat S 10.000 heeft. Ze zou graag 100.000 willen, maar ze weet dat B nooit een voorstel zal doen om te ruilen als B 100.000 bezit. Nu, S kan geen 1.000 hebben, want dat heeft B al. De enige conclusie die je kan trekken is dat S 100 heeft. B zou dus nooit moeten ruilen met S.
- What was in Stacey's box? Explain.
100.000 kan nooit; want S zou de ruil niet aangaan.
10.000 kan nooit; het argument hierboven verklaart dat ze alleen zou willen ruilen met 100.000, dit zal nooit worden aangeboden, dus ze zal altijd ‘nee’ zeggen tegen ruilen.
1.000 kan S niet bezitten; deze heeft B al.
De enige conclusie die overblijft, is de S het 100 bezit.
In Nathaniel's town, two competing stores advertise that they'll "match any competitor's advertisement," plus give a free gift of some value. Nathaniel's mom thinks it's great how much competition there is in town. Nathaniel disagrees with his mom's assessment of the situation and thinks there's little competition. You're brought in as an outside economic consultant. As an economist, which person do you agree with and why?
Antwoord
Je zou het eens moeten zijn met Nathaniel. In het geval dat bedrijf 1 weet dat bedrijf 2 zal prijs zal nabootsen (en andersom) is er voor geen bedrijven een directe aanleiding om te concurreren op prijs. Geen van de bedrijven heeft een ‘incentive’ om zijn prijs omlaag te doen. De concurrent zal dit onmiddellijk ook doen en het bedrijf zal nog steeds een helft van de markt pakken, alleen dan tegen een lagere prijs.
Harvey's wife, Martha (M), is always the one to decide their social schedule. She decides what to do, and, then, Harvey (H) decides whether to go. Harvey loves spending time with his wife, but he's tired of going to the symphony. Tonight, Harvey says, "I'm not going to go to the symphony again." Consider the extensive form of the game in the figure below. The payoffs of this game are (Martha's utility, Harvey's utility).
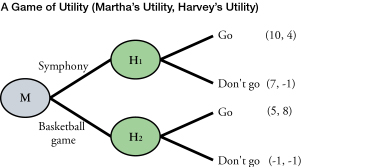
- Solve for the Nash equilibrium of the game.
- Is Harvey's threat credible?
Antwoord
- Solve for the Nash equilibrium of the game.
Hier kan weer de ‘backwards induction’ gebruikt worden. In het geval van H1 is ‘go’ de beste optie. In geval van H2 is ‘go’ ook de beste optie voor Harvey. Aangezien Martha dit weet zal Martha voor ‘Symphony’ kiezen en zullen we ze in het Nash-evenwicht met z’n tweeën naar de ‘symphony’ gaan.
- Is Harvey's threat credible?
Nee, aangezien Martha de ‘sympony’ altijd leuker vindt dan een basketbal wedstrijd, of Harvey nou besluit mee te gaan of niet.
Consider two firms, A and B. Firm A is considering whether to offer a sale. Firm B is considering whether to develop a new product. The payoff matrix below shows (profit to Firm B, profit to Firm A).
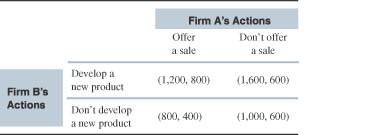
1. Does firm A have a dominant strategy? If so, what is it?
2. Does firm B have a dominant strategy? If so, what is it?
3. Solve for the Nash equilibrium of the game.
4. Is this game a Prisoner's Dilemma?
Antwoord
1. Does firm A have a dominant strategy? If so, what is it?
Bedrijf A heeft geen strikt dominante strategie, aangezien zijn beste keus afhangt van de keus van bedrijf B
2. Does firm B have a dominant strategy? If so, what is it?
Bedrijf B heeft een dominante strategie namelijk ‘develop a new product’. De uitbetalingen zijn altijd hoger (1200>800 en 1600>1000).
3. Solve for the Nash equilibrium of the game.
Als we het Nash-evenwicht oplossen dan krijgen we een evenwicht bij (‘develop a new product’, ‘offer a sale’).
4. Is this game a Prisoner's Dilemma?
Nee, er kan niet een grotere uitbetaling voor beiden ontstaan door af te wijken (oftewel, een onderlinge afspraak te maken) van het NE.
Two players: The employee (Raquel) and the employer (Vera). Raquel has to choose whether to pursue training that costs $1.000 to herself or not. Vera has to decide whether to pay a fixed wage of $10.000 to Raquel or share the revenues of the enterprise 50:50 with
Raquel. The output is positively affected by both training and revenue sharing. Indeed, with no training and a fixed wage total output is $20.000, while if either training or profit sharing is implemented the output rises to $22; 000. If both training and revenue sharing are implemented the output is $25.000.
1. What are the characteristics of the game?
2. Write this game in the normal form
3. Is there any equilibrium in dominant strategies?
4. Can you solve this game by IESDS?
5. Is there any Nash equilibrium?
Antwoord
1. What are the characteristics of the game?
Spelers: R & V
Strategieën: R: het volgen van de training (kosten1.000), of niet.
Strategieën: V: het geven van een vast salaris van 10.000 of het delen van de winst 50/50.
Uitbetaling: Hangt af van twee factoren: of R de training volgt en hoe V de winst verdeeld.
- Vast salaris + geen training: 20.000
- Vast salaris + wel training 22.000
- 50/50 split + geen training 22.000
- 50/50 split + training 25.000
2. Write this game in the normal form
Hierbij wordt gekeken naar speler 1 R en speler 2 V.
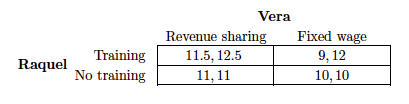
3. Is there any equilibrium in dominant strategies?
Nee, wat er zijn niet genoeg dominante strategieën om te spelen. V heeft een dominante strategie (’revenue' ‘sharing’), maar R niet.
4. Can you solve this game by IESDS? Is this game DS?
Ja, ‘fixed wage’ is voor V een gedomineerde strategie. Streep deze weg. Gegeven dat er perfecte informatie is en R weet dat V nooit de strategie ‘fixed wage’ zal spelen heeft R ook een gedomineerde strategie. R kan namelijk haar opbrengsten vergroten door training te verkiezen boven geen training. De strategie ‘training’ is dan een gedomineerde strategie. Als je deze ook wegstreept, dan blijft alleen (‘Training’, ‘Revenue sharing’) over. Dit spel is dus IESDS.
5. Is there any Nash equilibrium?
Ja. Dit evenwicht is het zelfde als IESDS.
Firms Alpha and Beta serve the same market. They have constant average costs of $2 per unit. The firms can choose either a high price ($10) or a low price ($5) for their output.
When both firms set a high price, total demand = 10,000 units which is split evenly between the two firms. When both set a low price, total demand is 18,000, which is again split evenly.
If one firm sets a low price and the second a high price, the low priced firm sells 15,000 units,
the high priced firm only 2,000 units.
Analyse the pricing decisions of the two firms as a non-co-operative game.
1. In the normal from representation, construct the pay-off matrix, where the elements of each cell of the matrix are the two firms' profits.
2. Derive the equilibrium set of strategies.
3. Explain why this is an example of the prisoners' dilemma game.
Antwoord
1. In the normal from representation, construct the pay-off matrix, where the elements of each cell of the matrix are the two firms' profits.
Eerst wordt er gekeken naar de uitbetalingen van de bedrijven:
- (hoge prijs, hoge prijs). De totale vraag is 10.000. Dus elk bedrijf verkoop 5.000 stuks.
Bedrijven maken een winst van 5000x(10-2) = 40.000.
- (lage prijs, lage prijs). De totale vraag is 18.000. Dus elk bedrijf verkoop 9.000 stuks.
Bedrijven maken een winst van 9000x(5-2) = 27.000
- (hoge prijs bedrijf A, lage prijs bedrijf B)
Bedrijf A: 2000x8 = 16.000
Bedrijf B: 15.000x3 = 45.000
- (lage prijs bedrijf A, hoge prijs bedrijf B)
Bedrijf A: 15.000x3 = 45.000
Bedrijf B: 2000x8 = 16.000
Kortom de uitbetalingsmatrix is als volgt:
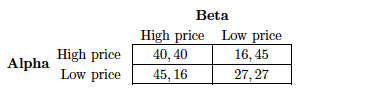
2. Derive the equilibrium set of strategies.
Elke speler heeft een dominante strategie, namelijk ‘low price’. Het evenwicht is dus (‘low price’, ‘low price’), oftewel (27,27)
3. Explain why this is an example of the prisoners' dilemma game.
Dit spel heeft belangrijke kenmerken van het ‘prisoners’ dilemma’:
Elke speler heeft een dominante strategie (‘low price’) maar beiden spelers kunnen hun uitbetalingen verhogen door samen te werken en allebei een hoge prijs te vragen. Het evenwicht (‘high price’, ‘high, price’) is een Pareto verbetering.
There are three players, 1, 2 and 3, and three alternatives, A, B and C. Players vote simultaneously for an alternative; abstaining is not allowed. Thus, the strategy spaces are Si = { A, B, C }. The alternative with the most votes wins; if no alternative receives a majority, then alternative A is selected. The payoff functions are:
U1 (A) = U2 (B) = U3(C) =2
U1 (B) = U2 (C) = U3(A) =1
U1 (C) = U2 (A) = U3(B) =0
- Find all the Nash equilibriums of this game
Antwoord
Eerst even alles op een rijtje zetten:
- Er zijn 3 spelers, dit is dus geen normaal spel zoals we gewend zijn met 2 spelers!
- Er zijn 3 alternatieven
- Dit is een spel waar men tegelijkertijd reageert; men kan dus niet de acties van een andere speler vooraf observeren
- Het alternatief met de meeste stemmen wint
- Als alle alternatieven evenveel stemmen krijgen, dan wint A
Hoe worden in dit spel de Nash-evenwichten gevonden?
Speler 1 heeft een voorkeur van A als uitkomst, daarna B en vervolgens C.
Speler 2 heeft een voorkeur voor B als uitkomst, daarna C en vervolgens A.
Speler 3 heeft een voorkeur voor C als uitkomst, daarna A en vervolgens B.
Uiteraard het eerst uitgetekend worden in een normale vorm (matrix). Dit is moeilijker omdat je nu 3 spelers hebt. Je zal dan ook niet 1 matrix moeten uittekenen, maar 3.
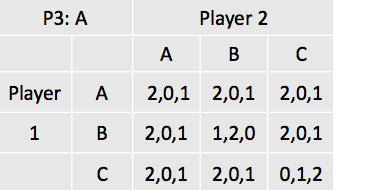
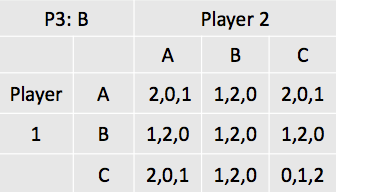
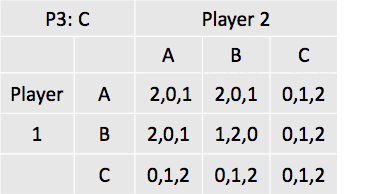
Linksboven staan telkens de keuzes van speler 3 beschreven. Zie bijvoorbeeld matrix 1. Als alle drie de spelers A kiezen, dan krijgt speler 1 een uitbetaling van 2, speler 2 een uitbetaling van 0 en speler 3 een uitbetaling van 1 (zie de uitbetalingsfuncties).
Nu kan het Nash-evenwicht gevonden worden door alle matrices af te werken. Eerst wordt er gekeken naar het maximaliseren van de uitbetaling van speler 1, gegeven want speler 2 en 3 doen. Gegeven dat speler 3 A kiest, en speler 2 A, maakt het voor speler 1 qua uitbetaling niet uit of hij A, B of C kiest. Zet dus een streep onder alle drie de ‘2tjes’. Mocht speler 3 a kiezen, maar speler 2 B, dan maximaliseert speler 1 zijn uitbetaling door of A of C te spelen. Als je dit proces vervolgt dan krijg je de volgende oplossingen:
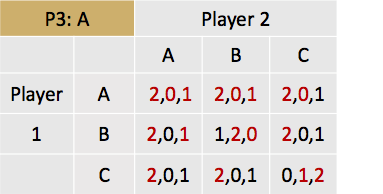
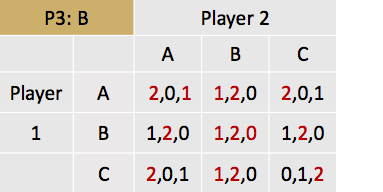
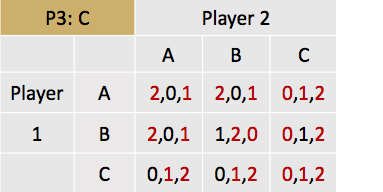
De Nash-evenwichten die zijn ontstaan zijn als volgt:
(A,A,A)
(A,B,A)
(B,B,B)
(A,C,C)
(C,C,C)
- For the given game, iteratively eliminate all strictly dominated strategies.
- Is this game DS?
- Find all pure NE.
Antwoord
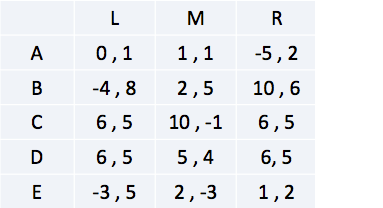
1. For the given game, iteratively eliminate all strictly dominated strategies.
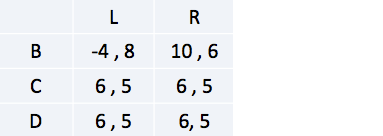
Er moet worden gekeken of er strikt gedomineerde strategieën in het spel zitten die geëlimineerd kunnen worden. Het is handig om eerst te kijken bij de speler die de minste optionele strategieën heeft (in dit geval speler 2).
Speler 2: Je ziet dat strategie R altijd beter is dan de strategie M. Strategie M is dan ook strikt gedomineerd door R. Verwijder deze dus.

Speler 1: Zowel strategie C als D strikt domineren de strategie A en E. Je kan A en E dus elimineren.
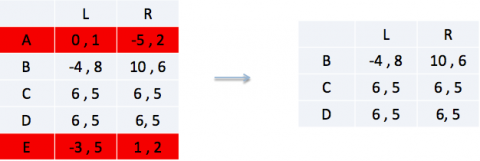
Er zijn nu geen strikt gedomineerde strategieën meer aangezien de uitbetaling van B in het geval dat speler 1 R kiest groter is dan die van C en D. Oftewel, het oplossing stopt hier. Een unieke oplossing door middel van IESDS is niet mogelijk.
2. Is this game DS?
We moeten nu de zwak gedomineerde strategieën elimineren. We kunnen gewoon de laatste matrix van de IESDS methode gebruiken aangezien een strikt gedomineerde strategie ook per definitie een zwak gedomineerde strategie is.
Speler 2: Voor deze speler is R een zwak gedomineerde strategie door L.
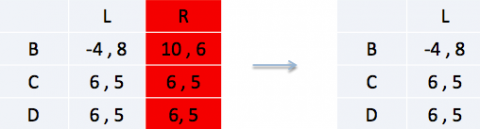
Speler 1: Voor deze speler is de strategie B strikt gedomineerd door zowel C als D.

In dit geval vinden we een DS spel waarin zowel (C,L) als (D,L) evenwichten zijn. In dit geval gaat de regel op dat de uitbetaling voor beide spelers gelijk zijn, kortom de DS methode is te gebruiken.
3. Find all pure NE.
Er zijn twee Nash evenwichten te vinden:
(C,L)
(D,L).
Let players play the following game:
The game is common knowledge, but players’ rationality is not.
Each player only knows that he is rational, and that his opponent is also rational.
1. Can you predict which strategy player 1 will play? Which pay-off will he get?
2. Can you predict which strategy player 2 will play? Which pay-off will he get?
3. Is this game DS under common knowledge?
4. Find all (pure and mixed) NE.

Antwoord
- Can you predict which strategy player 1 will play? Which pay-off will he get?
- Can you predict which strategy player 2 will play? Which pay-off will he get?
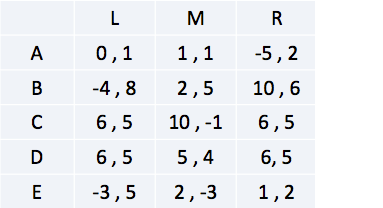
Gegeven dat spelers rationeel zijn kan er gekeken worden welke strategieën ze nooit zal spelen; oftewel er wordt gekeken welke strategieën (zwak) gedomineerd worden.
Speler 2:
Strategie M wordt sterk gedomineerd door strategie R.
Speler 1:
Gegeven dat speler 1 weet dat speler twee nooit strategie M zal spelen zal hij kijken naar wat voor hem het beste is. Er kan worden gesteld dat speler 1 een dominante strategie heeft, namelijk strategie C. Deze strategie is beter dan strategie A, B, D en E. Kortom, speler 1 elimineert deze strategieën.
Speler 2:
Gegeven dat speler 2 weet dat speler 1 deze strategieën zal elimineren heeft speler 2 de keuze tussen (C, L) of (C, R). Voor speler 2 maakt de uitbetaling niet uit; beiden zijn 5. Dus speler 2 is willekeurig tussen deze twee strategieën; hij zal er random eentje kiezen. Let op, in dit spel wil iedereen zijn eigen winsten maximaliseren; speler 2 is er dus niet op uit om speler 1 winsten te minimaliseren.
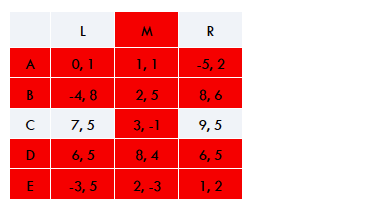
Kortom,
De uitbetaling voor speler 1 is ½ x 7 + ½ x 9 = 8
De uitbetaling voor speler 2 is 5.
3. Is this game DS under common knowledge?
Alle zwak gedomineerde strategieën worden geëlimineerd. Zoals hierboven aangegeven blijven, als alle gedomineerde strategieën weg worden gehaald, (C,L) en (C,R) over. Dit spel is dus niet DS, aangezien de antwoorden van deze vakjes niet identiek zijn voor alle spelers.
4. Find all (pure and mixed) NE.
De Nash-evenwichten zijn in dit geval gelijk aan de evenwichten die we vonden bij vraag 1 en 2. (C,L) en (C,R).
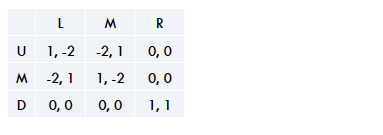
Does this game has a pure NE?
Does this game have mixed NE?
Antwoord
1. Does this game has a pure NE?
Een uniek puur NE betekent dat er maar 1 NE in het spel zit; de speler bedeelt dus de kans ‘1’ aan de strategie die tot dit evenwicht komt toe.
In dit geval komen door middel van het zetten van streepjes erachter dat dit evenwicht (D,R) is.
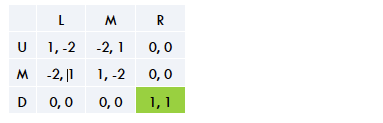
2. Does this game have mixed NE?
In het geval van een gemixte strategie bedelen de speler kansen toe aan het kiezen van een bepaalde strategie.
Een Nash-evenwicht in een gemixte strategie houdt in dat: Ui (a*) ≥ Ui(ai,a*-i) voor elke gemixte strategie ai van speler i.
In ons geval bedelen we de volgende kansen toe:
Pr (U) = p
Pr (M) = q
Pr (D) = 1 – p – q
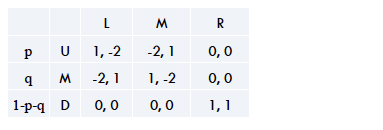
De uitbetalingen van speler 2 kunnen nu worden bepaald. Als speler 2 de strategie L speelt, dan is zijn uitbetaling (-2xp) + (1xq) + (0x [1-p-q]). Dit kan ool worden gedaan voor strategie M en R doen:
U2 (L) = -2p + q
U2 (M) = p – 2q
U2 (R) = 1-p-q
Er kan worden uitgegaan van: p > 0 en q > 0.
De ‘utility’ (U) van een strategie moet gelijk zijn aan een (U) van een andere strategie, aangezien men anders de ene met een kans van 1 boven de ander zou verkiezen. Oftewel, de speler moet qua ‘utility’ onwillekeurig zijn tussen twee strategieën. Als hij dat niet is, dus als de ene strategie meer ‘utility’ opbrengt dan de ander, zou de speler rationeel gezien altijd voor degene kiezen met de meeste verwachte ‘utility’.
Dus U2 (L) = U2 (M)
-2p + q = p – 2q
-2p + q – p + 2q = 0
-3p + 3q = 0
-3p = -3q
p = q
U2 (L) = U2 (R)
-2p + q = 1-p-q
-2p + p = 1 – 2q
-p = 1 – 2q
p = -1 + 2q
U2 (M) = U2 (R)
p – 2q = 1-p-q
2p = 1 + q
p = ½ + ½ q
Virtually any textbook on economic models postulate the so-called “Law of One Price”, which states that identical goods have to be sold at identical prices. Everybody (except some economists though) knows that this is not true. Virtually any retail market is characterized by price dispersion. Why do we observe price dispersion? One of the possible explanations is heterogeneity of consumers’ information: some of consumers know more about the market than the other. Here is the model that has this feature.
Two identical firms produce and sell homogeneous good with zero production costs. Firms simultaneously call (non-negative) prices p1 and p2. There is a unit mass of consumers. Each consumer has a valuation v > 0 for the good (the maximum price that they ever want to pay). A fraction of λ consumers is informed about prices and buy at the lowest price (if the prices are equal they split evenly between the firms). A fraction of (1- λ) consumers is uninformed, they just buy the good at the closest store. We assume that they split evenly between the firms.
1. Is p1 = p2 = 0 NE? Why?
2. Is p1 = p2 = v NE? Why?
3. Is p1 = p2 = p for all (0, v) NE? Why?
4. Can p1 > p2 or p1
Suppose that firms plays mixed strategies F1 and F2, i.e., price P1 is random variable with the distribution function F1: Pr(Pi ≤ x) = x for x for all (p*1, p#1), where p*1 and p#1 are respectively the lowest and highest price charged by firm i. Suppose that both F1 and F2 are continuous distributions (without mass points).
5. Can it be that P*1 P*2 ? What does it mean?
6. Can it be that P#1 > v
7*. Can it be that P#1 ≤ P#2
8*. Math starts only here: compute pay-off function.
Antwoord
In dit voorbeeld wordt er uitgegaan van een Betrand competitie. Dit is een competitie door middel van prijzen (zoals Cournot door middel van hoeveelheden gaat). De bedrijven geven gelijkertijd en onafhankelijk van elkaar hun prijzen p1 en p2. De consumenten hebben een maximale prijs die ze willen betalen voor het project: dit is v > 0. Verder is er sprake van asymmetrisch informatie. De ene groep consumenten weet meer dan de andere groep. De fractie λ is volledige op de hoogte van de prijzen in de markt en logischer wijs 1 - λ is niet volledige op de hoogte van de prijzen in de markt. Deze laatste groep zal dus waarschijnlijk naar de dichtbij zijnde winkel gaan op het product tegen prijs p1 of p2 te halen.
1. Is p1 = p2 = 0 NE? Why?
Als beiden bedrijven hun producten aanbieden voor de prijs van 0, dan maken beiden bedrijven geen winst. Echter, kunnen ze afwijken van de prijs van nul en zo de fractie consumenten binnenhalen die niet volledige informatie hebben over de prijzen in de markt. Beiden bedrijven zullen dan de helft van fractie 1 – λ binnenhalen. De winst die het bedrijf dan maakt is (1 – λ / 2 )v. Dit is echter geen Nash evenwicht, aangezien bij prijzen van 0 de bedrijven een mogelijkheid hebben om hun winsten te verhogen door af te wijken. Het Nash evenwicht stelt dat bedrijven niet willen afwijken van het evenwicht. Dat gaat in dit geval niet op.
2. Is p1 = p2 = v NE? Why?
In dit geval is de prijs van bedrijf 1 gelijk aan de prijs van bedrijf 2, beiden bedrijven maken dus wel winst. Echter, het is lucratief voor een bedrijf om van dit evenwicht af te wijken. Als het bedrijf net onder p1 = p2 = v gaan zitten dan zal het de gehele geïnformeerde markt (λ) naar zich toetrekken en daardoor de winsten verhogen. Het is dus weer geen Nash-evenwicht.
3. Is p1 = p2 = p for all (0, v) NE? Why?
Eigenlijk is deze vraag een generalisatie van de vorige twee vragen; het is voor beiden bedrijven lucratief om af te wijken van dit evenwicht.
4. Can p1 > p2 or p1
Denk hierbij aan het voorbeeld dat bedrijf 1 een prijs vraag van 2 en bedrijf 2 een prijs vraagt van 4. Het is voor bedrijf 1 altijd lucratief om een hogere prijs te vragen, maar wel een prijs die zich nog onder de 4 bevindt. Aangezien het bedrijf 1 dan nog steeds zijn marktaandeel behoudt, maar ditzelfde marktaandeel wel een hogere prijs betaalt. Oftewel, dit is weer geen Nash-evenwicht.
5. Can it be that P*1 P*2 ? What does it mean?
Deze gemixte strategieën worden gegeven omdat er door middel van een gemixte strategie wel een Nash-evenwicht kan ontstaan.
In dit geval speelt bedrijf 1 de gemixte strategie F1(p) en bedrijf 2 de gemixte strategie F2(p). Let op dat in de verdeling van de prijzen er alleen prijzen tussen de 0 en V worden genomen (Pr(Pi ≤ x) = x voor x voor alle (p*1, p#1), waar p*1 en p#1 respectievelijk de laagste en de hoogste prijzen zijn, bereikt door bedrijf i).
Kan het voorkomen dat P*1
6. Can it be that P#1 > v
In dit geval is de vraag of de hoogste prijs waaraan bedrijf i een kans toebedeelt groter kan zijn dan v, de waarde van de consumenten. Dit kan niet, de consument zal dan het product niet kopen en het bedrijf maakt geen winst. Dit kan het bedrijf echter veranderen door net onder v te gaan zitten. In een gemixte strategie moet de uitbetaling van de strategieën van bedrijf i gelijk zijn (anders zou hij een kans toebedelen van 1 aan de strategie die het beste werkt). Kortom, de ongelijkheid van P#1 > v kan niet bestaan.
7. Can it be that P#1 ≤ P#2
Ook dit kan niet ontstaan. Aangezien bedrijf 2 zijn winst kan verhogen door in plaats van prijs P#2 de prijs v te vragen. Hetzelfde geldt voor bedrijf 1. Er ontstaat P#1 = P#2 = v. Deze prijs zal ergens liggen tussen 0 en v.
8. Math starts only here: compute pay-off function.
De bedrijven krijgen winst uit twee marktsegmenten:
Zie hier bedrijf 2:
- De ongeïnformeerde consumenten: ((1 – λ)/2) P2
- De geïnformeerde consumenten: λ P2
Echter gaat 2 alleen maar op als bedrijf 2 ook daadwerkelijk de laagste prijs aanbiedt. Dit is een kans van 1 – F1(P2). Waarom? Aangezien bedrijf 1 zijn gemixte strategie F1(P) kiest, is de kans dat daarbij P1 > P2 gelijk aan 1 – F1(P2). De winst is dus: (1-F1(P2)) λ P2.
Als we 1 en 2 bij elkaar optellen krijgen we de totale winstfunctie:
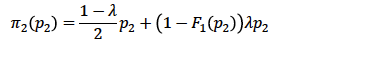
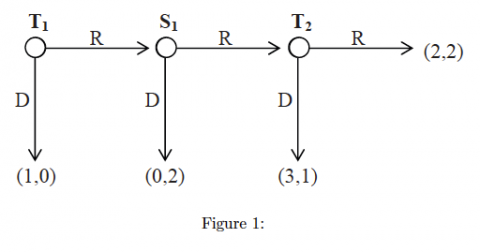
Trinny and Susannah are playing the ”Centipede” game. At each node in the game the player can either move down, which means the game stops, or move right, which means that the game is passed to the other player. The two cycle game is depicted in Figure 1. Trinny’s pay-off is given first.
1. Solve the game by backward induction
2. Show that the outcome is inefficient.
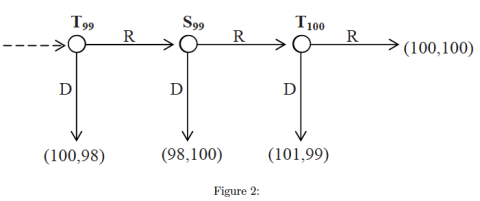
3. If the game was extended to 100 cycles, with the pay-offs increasing in a similar manner, as represented in Figure 2, how would this affect the outcome of the game? What happens if T1 chooses right instead of down?
Antwoord
1. Solve the game by backward induction
Het eerste spel wordt opgelost door ‘backward induction’.
1e sub-spel – T1 moet een keuze maken: D (3,1)
2e sub-spel – S1 moet een keuze maken: gegeven dat S1 weet dat T1 voor D zal kiezen kan S1 zijn uitbetaling maximaliseren door D te kiezen (0,2)
3e sub-spel – T1 moet een keuze maken: gegeven dat T1 weet dat S1 is het volgende spel voor D zal kiezen (uitbetaling voor T1 is dan 0), zal T1 zijn winst maximaliseren door D te kiezen (1,0).
De oplossing van het spel is dat T1 direct voor D kiest. Het spel stopt en de uitbetaling is (1,0). Kortom, 1 voor T1 en 0 voor S1.
2. Show that the outcome is inefficient.
De uitbetaling van (1,0) kan Pareto verbeterd worden door (3,1) en (2,2).
3. If the game was extended to 100 cycles, with the pay-offs increasing in a similar manner, as represented in Figure 2, how would this affect the outcome of the game? What happens if T1 chooses right instead of down?
Het zou het spel niet beïnvloeden. Het spel stopt na de eerste zet.
Als T1 de actie ‘rechts’ kiest dan dat komen door:
- T begrijpt het spel niet
- Begrensde rationaliteit – T heeft het spel nog niet helemaal uitgewerkt
- Altruïsme – T gunt S meer uitbetaling
- T wil misschien een samenwerking aangaan en geeft een signaal
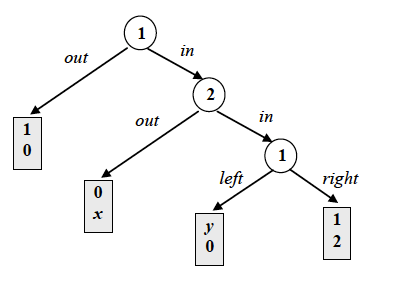
Consider only pure NE and SPNE here:
1. Assume y for all numbers between 0 and 1. Find NE and SPNE for x for all numbers between 0 and 2.
2. Again assume y for all number between 0 and 1. Find NE and SPNE for x is 2.
3. Suppose y = 1. Find NE and SPNE for x = 0.
Antwoord
Dit is net zoals het vorige spel een ‘in’ or ‘out’ spel.
1. Assume y for all numbers between 0 and 1. Find NE and SPNE for x for all numbers between 0 and 2
Eerst zal er opzoek worden gegaan naar de SPNE door middel van ‘backwards induction’:
1e sub-spel: Hier mag speler 1 kiezen (onderste sub-spel)
Speler 1 zal voor ‘right’ gaan, aangezien zijn uitbetaling dan zeker 1 is, in tegenstelling tot een getal tussen 0 en 1.
2e sub-spel: hier mag speler 2 kiezen
Speler 2 zal voor ‘in’ kiezen aangezien hij weet dat het volgende sub-spel speler 1 voor ‘right’ kiest en hij zijn uitbetaling van 2 kan veilig stellen.
3e sub-spel: hier mag speler 1 kiezen (bovenste sub-spel)
Speler 1 zal onwillekeurig zijn tussen ‘in’ en ‘out’ aangezien beiden een uitbetaling opleveren van 1.
De SPNE zijn dus:
((In, right),in) en ((Out, right),in)
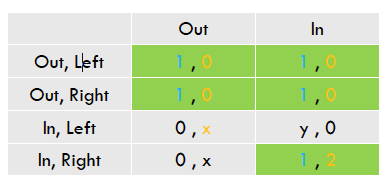
Nu wordt er gekeken naar de pure Nash-evenwichten:
Er wordt een normaal vorm spel getekend om dit te achterhalen
2. Again assume y for all number between 0 and 1. Find NE and SPNE for x = 2.
Eerst zal er opzoek worden gegaan naar de SPNE door middel van ‘backwards induction’:
1e sub-spel: Hier mag speler 1 kiezen (onderste sub-spel)
Speler 1 zal voor ‘right’ gaan, aangezien zijn uitbetaling dan zeker 1 is, in tegenstelling tot een getal tussen 0 en 1.
2e sub-spel: hier mag speler 2 kiezen
Speler 2 zal voor ‘out’ aangezien x > 2. Deze uitbetaling is voor speler 2 dus hoger dan wanneer hij doorgaat met het spel en uitbetaling van 2 behaald.
3e sub-spel: hier mag speler 1 kiezen (bovenste sub-spel)
Gezien speler 1 weet dat speler 2 in de volgende zet ‘out’ zal kiezen (een uitbetaling van 0 voor speler 1) zal speler 1 de actie ‘out’ kiezen.
De SPNE zijn dus:
((‘Out’, ‘right’),’out’)
Nu kijken we naar de pure Nash-evenwichten:
Er wordt een normaal vorm spel getekend om dit te achterhalen
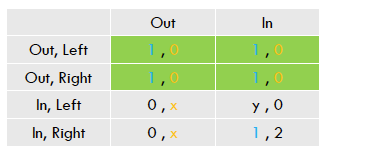
Hieruit kan gesteld worden dat 1 NE wegvalt.
3. Suppose y = 1. Find NE and SPNE for x = 0.
Eerst zal er opzoek worden gegaan naar de SPNE door middel van ‘backwards induction’:
1e sub-spel: Hier mag speler 1 kiezen (onderste sub-spel)
Aangezien y > 1 dan 1 zal speler 1 voor ‘left’ kiezen.
2e sub-spel: hier mag speler 2 kiezen
Speler 2 zal voor ‘out’ kiezen (uitbetaling x>0) aangezien hij weet dat als hij doorspeelt speler 1 voor ‘left‘ zal kiezen en speler 1 een uitbetaling van 0 zal bemachtigen.
3e sub-spel: hier mag speler 1 kiezen (bovenste sub-spel)
Speler 1 zal voor ‘out’ kiezen aangezien hij weet dat speler 2 in de volgende zet voor ‘out’ kiest en hij anders een uitbetaling van 0 krijgt, in plaats van 1.
De SPNE zijn dus:
((‘Out’, ‘left’),’out’)
Nu kan er worden gekeken naar de pure Nash-evenwichten:
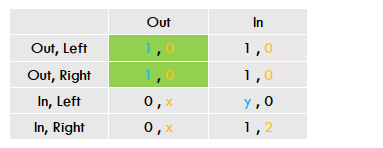
Er wordt een normaal vorm spel getekend om dit te achterhalen
Two players play the following game.
Player 1(2) and his pay-offs are denoted by white (black) circles and numbers.
1. Find SPNE of this game.
Antwoord
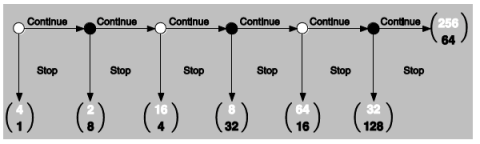
1. Find SPNE of this game.
Dit gebeurd weer door middel van ‘backward induction’.
6e spel: Speler 2 kiest ‘stop’.
5e spel: Speler 1 kiest ’stop’.
4e spel: Speler 2 kiest ‘stop’.
3e spel: Speler 1 kiest ’stop’.
2e spel: Speler 2 kiest ‘stop’.
1e spel: Speler 1 kiest ’stop’.
Kortom, het SPNE is ({‘always play stop’}, {‘always play stop’}) met een uitbetaling van (4,1)
We consider a Cournot model with two firms, a duopoly. They produce a homogeneous good. The strategies are quantities. Firm 1 and firm 2 chose simultaneously their output levels, q1. They sell their output at the market-clearing price p(q), where Q = q1 + q2. Firm i’s cost of production is ci(qi) and firm i’s total profit is then: Ui (q1,q2) = qip(q) – ci(qi).
The market demand is given by:
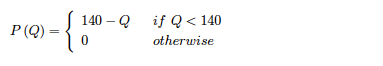
The unit costs are given by 20$.
- Define the reaction (best response) functions of the firms
- Find the Cournot equilibrium
- Define the Nash equilibrium.
Antwoord
In deze opgave draait het om het Cournot evenwicht. Eerst wordt alle informatie op een rijtje gezet:
Hoeveelheid:
Bedrijf 1: q1 ≥ 0
Bedrijf 2: q2 ≥ 0
Totale hoeveelheid Q = q1 + q2
Prijs:
Prijs bij verkoop totale hoeveelheid: p = a−q1 −q2.
a = marktvraag = 140
Kosten:
Er zijn alleen variabele kosten (aangezien c afhangt van de output q):
0
Bedrijf 1: c1(q1)
Bedrijf 2: c2(q2)
Unit kosten: 20$
Winst:
Bedrijf 1: q*p - cq = q1(a − q1 − q2) − cq1 als q1 + q2 ≤ a, en 0 anders
Bedrijf 2: q*p - cq = q2(a − q1 − q2) − cq2 als q1 + q2 ≤ a, en 0 anders
1. Define the reaction (best response) functions of the firm
In een Cournot duopolie is de reactie van Bedrijf 1 een optimale respons op de reactie van bedrijf 2. Dit betekent dat bedrijf 1 zijn winst maximaliseert gegeven wat bedrijf 2 produceert.
Bedrijf 1: q*p - c = q1(a − q1 − q2) − cq1 als q1 + q2 ≤ a, en 0 anders
q1(140 – q1 – q2) – 20q1
Om dit te maximaliseren bepalen we de eerste afgeleiden (differentiëren).
Daarvoor wordt eerst de winst uitgeschreven
140q1 – q1^(2) – q1q2 – 20q1
1e afgeleiden van winst naar q1:
140 – 2q1 – q2 – 20
Gelijk stellen aan nul:
140 – 2q1 – q2 - 20 = 0
2q1 = 140 – q2 - 20
q1 = (140 – q2 – 20)/2
Aangezien dit spel symmetrisch is heeft elk bedrijf dezelfde kosten functie en dezelfde reactie functie:
q2 = 60 – [ (q1)/2 ]
- Find the Cournot equilibrium
Het Cournot evenwicht wordt bepaald door de hoeveelheid waarbij het voor elk bedrijf de beste reactie is op de ander. q1* = q2*
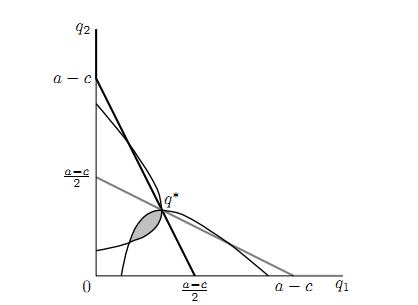
Het snijpunt van de lijnen kunnen worden berekend:
q1* = q2*
Eerst gebeurd dit algebraïsch, omdat je vervolgens gemakkelijk een formule kan afleiden en deze kan invullen met de getallen die in de opgave gegeven zijn:
q1 = (a − c − q2)/2 en q2 = (a − c − q1)/2.
De oplossing van het snijpunt is als volgt:
q1*=q2*= 1/3 (a-c).
Invullen:
1/3 (140 – 20) = 40
Dus q1* = q2* = 40
De totale hoeveelheid geproduceerd in de markt bedraagt dan:
Q* = q1* + q2* = 80
De evenwichtsprijs is:
p = a−q1 −q2.
P = 140 – 40 - 40 = 60
De winsten van de bedrijven bedragen:
Winst: q*p – cq
(60x40) – (20x40)
2400 – 800 = 1600
- Define the Nash equilibrium
Een Nash-evenwicht in dit spel is, net als bij de voorgaande simpelere spellen, een vaste staat; geen elke speler zal afwijken. Dat betekent in dit geval een paar (q1, q2) zodanig dat, gegeven q2, de strategie q1 de winst van bedrijf 1 maximaliseert en, gegeven q1, de strategie q2 de winst van bedrijf 2 maximaliseert.
In dit spel is het Cournot evenwicht een Nash-evenwicht. Waarom? Aangezien geen van beiden speler zou willen afwijken van dit evenwicht. Geen van de twee bedrijven zal het beter doen als het bedrijf afwijkt van de totale geproduceerde hoeveelheid in het Cournot evenwicht.
Aangezien dit onderwerp bij het tentamen een belangrijke rol speelt nog even op een rijtje wat er precies is gedaan hierboven:
- Eerst wordt er een ‘best respons functie’ gemaakt. De winsten van de bedrijven zijn hiervoor nodig.
Winstfunctie bedrijf 1: q1(a − q1 − q2) − cq1 vereenvoudigen
- = q1(a − q1 − q2 − c)
- = q1a – q1^(2) – q1q2 – q1c
- afgeleide naar q1 bepalen
- = a − 2q1 − q2 – c
- afgeleide gelijk stellen aan 0
- q1 = (a – q2 − c) / 2
Kortom:
Bedrijf 2:
als q2 ≤ a – c q1 = (a − q2 − c)/2
als q2 > a – c q1 = 0
Bedrijf 1:
als q1 ≤ a – c q2 = (a − q2 − c)/2
als q1 > a – c q2 = 0
Vervolgens bereken we het snijpunt van q1* = q2*:
- Spijpunt van de lijnen berekenen
- q1 = (a − c − q2)/2 en q2 = (a − c − q1)/2.
- q1 = (a − c − q2)/2 = q2 = (a − c − q1)/2.
- Oplossen van de vergelijkingen
- q1*=q2*= 1/3 (a-c).
In de uitwerkingen zag je dat 1/3 (140 – 20) = 40.
In a market characterized by the following (inverse) demand function
P = 40 - Q
Two firms compete a la Cournot. Firm A has production cost described by the cost function
ca (qa) = 20qa, while firm B's cost function is cB (qB) = qb^(2).
1. Which firms has increasing marginal cost? Which one has constant marginal cost?
2. Define the reaction functions of the firms.
3. Compute the Cournot equilibrium quantities and price.
Antwoor
In deze opgave draait het om het Cournot evenwicht. Eerst weer even alle informatie op een rijtje:
Hoeveelheid:
Bedrijf 1: q1 ≥ 0
Bedrijf 2: q2 ≥ 0
Totale hoeveelheid Q = q1 + q2
Prijs:
Prijs bij verkoop totale hoeveelheid: p = 40 - Q
a = marktvraag = 40
Kosten:
Er zijn alleen variabele kosten (aangezien c afhangt van de output q):
0
Bedrijf A: 20qa
Bedrijf B: qb^(2).
Winst:
Bedrijf A: qa*p - cqa = qa*(40-(qa+qb) - 20qa
Bedrijf B: qb*p - cqb = qb*(40-(qa+qb) - qb^(2)
1. Which firms has increasing marginal cost? Which one has constant marginal cost?
De marginale kosten kan je bepalen door de afgeleide te bepalen:
MC bedrijf A: 20 deze is constant en onafhankelijk van qa
MC bedrijf B: 2qb deze vergroot naarmate qb groter wordt.
2. Define the reaction functions of the firms.
Nu moeten de reacties van de functies worden bepaald (best responseDit gebeurd op dezelfde manier waarop dit in de vorige opgave ook is gedaan.
- Eerst wordt er een ‘best respons functie’ gemaakt. De winsten van de bedrijven zijn hiervoor nodig
- Winstfunctie bedrijf 1 vereenvoudigen
- Afgeleide naar q1 bepalen
- Afgeleide gelijk stellen aan 0
- Herschrijven naar q1
We beginnen bij bedrijf A:
- Winstfunctie: qa*(40-(qa+qb) - 20qa
- 40qa – qa^(2) – qaqb – 20qa
20qa – qa^(2) – qaqb
- Afgeleide: 20 – 2qa – qb
- 20 – 2qa – qb = 0
- -2qa = -20 + qb à qa = (20 – qb) / 2
Hetzelfde doen we voor bedrijf B:
- Winstfunctie: qb*(40-(qa+qb) - qb^(2)
- 40qb – qbqa – qb^(2) – qb^(2)
40qb – qbqa – 2qb^(2)
- Afgeleide: 40qb – qa – 4qb
- 40 – qa – 4qb = 0
- -4qb = -40 + qa à qb = (40 – qa) / 4
De ‘best-response’ functies zijn dus:
Bedrijf A: qa = (20 – qb) / 2
Bedrijf B: qb = (40 – qa) / 4
3. Compute the Cournot equilibrium quantities and price.
Nu wordt het snijpunt van q1* = q2*:
- Snijpunt van de lijnen berekenen
- De ‘best-response’ functies oplossen (substitutie)
- Oplossen van de vergelijkingen
- q1*≠q2*
- Prijs berekenen met P = 10 – Q
- De winsten van de bedrijven berekenen
Te beginnen met de functies uit vraag 2:
- (20 – qb) / 2 en (40 – qa) / 4
- qa = [ (20 – ((40 – qa) / 4)) ] / 2
- qa* = 40/7 en qb* = 60/7
- Klopt
- P = 40 – (100/7) = 180/7
- Winst bedrijf A = 180/7qa* - 20qa* = 1600/49
Winst bedrijf B = 180/7qa* - qb*^(2) = 7200/49
We consider a Betrand model with two firms, a duopoly. They produce a homogeneous good. The strategies are price. Firm 1 and firm 2 chose simultaneously their pricelevels.
The market demand is given by:
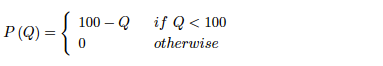
Suppose that two firms both have average variable cost c = $50. Assuming that firms compete in prices, then:
- Define the reaction (best response) functions of the firms
- Find the Betrand equilibrium
- Would your answer change if there were three firms? Why?
Antwoord
In dit geval heb je te maken met twee bedrijven die concurreren door middel van prijzen.
1. Define the reaction (best response) functions of the firms
Het construeren van de reactie functie in een Betrand competitie gaat als volgt:
Hiervoor wordt de vraagfunctie, van de markt, P = 100 – Q gebruikt.
Eerst wordt er gekeken naar bedrijf 1:
1. P1 > P2 Bedrijf 1 verkoopt niets en heeft 0 winst
2. P1 = P2 Bedrijf 1 verkoopt evenveel als bedrijf 2. Ze delen de markt.
Omzet = P x Q
Omzet = (P1 – 50) x Q
Omzet = (P1 – 50) x (100 – P1)
Bedrijf 1 bezit helft van de markt:
½ (P1 – 50) x (100 – P1)
3. P1
Omzet = (P1 – 50) x (100 – P1)
Nu worden de ‘grenzen van de prijs bepaald’.
1. P2
2. 50
Eerst bepaal je de monopolie prijs. Dit doe je door de afgeleide te nemen van (P1 – 50) x (100 – P1).
dw/dp1 = 150P1 – P1^(2) – 5.000
150 – 2p1 = 0
p1 = 75
Bedrijf 1 moet net onder de prijs van bedrijf 2 gaan zitten (P1 = P2 + e). Waarbij een ‘e’ een zeer klein getal is.
3. P2 > 75 Bedrijf 1 kan het beste precies op de monopolie prijs gaan zitten; het maximaliseert zijn winst.
De reactie funtie van zowel bedrijf 1 als bedrijf 2 is als volgt
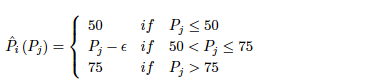
2. Find the Betrand equilibrium
Het NE ontstaat waar de twee reactiefuncties elkaar raken. Dit is in het punt P1 = P2 = 50. Dit is intuïtief ook logisch. Stel dat bedrijf 1 zijn prijs hoger zet dan 50, dan zal bedrijf 2 de hele markt kunnen pakken door zijn prijs net even iets onder 50 te zetten. Hierop reageert bedrijf 1 weer door zijn prijs iets onder die van bedrijf 2 te zetten. Dit proces zal doorgaan tot de evenwichtsprijs 50 wordt bereikt. Aangezien beiden bedrijven onder de prijs van 50 verlies maken, zal de prijs zich nooit onder 50 bevinden.
3. Would your answer change if there were three firms? Why?
In dit geval maakt het niet uit hoeveel bedrijven zich in de Betrand competitie bevinden, de evenwichtsprijs zal gelijk blijven aan de variabele kosten.
If two firms have the same constant marginal cost, they earn zero profits in the Bertrand equilibrium. This depends crucially on the feature that the goods involved are perfect substitutes. If products are differentiated instead, then the Bertrand equilibrium can lead to positive profits. The products are differentiated when consumers consider them only imperfect substitutes While a consumer may be unwilling to buy the product of one producer, she will have the incentive to do this if the price of their favorite product becomes too high. To model this we allow the demand for each good to depend not only on its own price but also on the price of the other good.
Assume for example that the demand for the good produced by Firm1, q1, and the demand for the good produced by Firm2, q2, are described by the following functions:
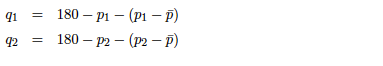
Where p with the stripe above is the average price that is taken over the prices of the two firms. Each firm has average (and marginal) cost c = 20. Suppose the firms can only choose between the three prices {94; 84; 74}.
1. Compute the profits of the firms under the 9 different price combinations that are possible in the model.
2. Using you answer to the previous point, construct the 3x3 payoff matrix for the normal form game where the payoffs are given by the profits of the firms
3. Find the (Bertrand-)Nash equilibrium of this game. What are the profits at this equilibrium?
Antwoord
In dit geval hangt de vraag van de consument ook af van de prijs van de concurrent.
1. Compute the profits of the firms under the 9 different price combinations that are possible in the model.
De winst van beiden bedrijven worden bepaald door Q1 x (P1- c). Stel de prijs voor Bedrijf 1 is 94 en voor bedrijf 2 is de prijs 84:
Winst bedrijf 1: (180 – 94 – (5)) x (94 – 20) = 81 x 74 = 5994. Op deze manier kan je dit voor elk bedrijf berekenen.
2. Using you answer to the previous point, construct the 3x3 payoff matrix for the normal form game where the payoffs are given by the profits of the firms
In de volgende matrix worden de berekende winsten neergezet:
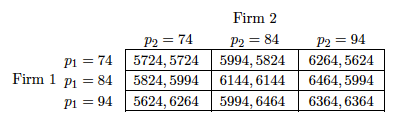
3. Find the (Bertrand-)Nash equilibrium of this game. What are the profits at this equilibrium?
Het Nash-evenwicht kan op de normale manier worden opgelost. Er is dan een NE van (p1 = 84, p2 = 84) oftewel een strategie van (84, 84), met de uitbetalingen van (6144, 6144).
Solve the Stackleberg model for 3 firms with zero costs that more one after another in the market with inverse demand p = 1 – Q.
Antwoord
Achter deze korte vraag zit een groot stuk theorie.
In het Stackelberg model zetten bedrijven na elkaar de ‘output’. Oftewel, bedrijven kunnen elkaar observeren en vervolgens reageren. De leider zet zijn ‘output level’ en de anderen zijn vrij om zijn optimale ‘output’ te kiezen gegeven zijn kennis over de leider.
Hoe kan je dit oplossen: ‘backward induction’. Er wordt dus begonnen bij het laatste bedrijf wat zijn prijs zet;
Bedrijf 3:
De vraagfunctie van bedrijf 3 is p = 1 – q1 – q2 – q3.
De winstfunctie van bedrijf 3 is winst = q3 x p oftewel winst = q3 x (1 – q1 – q2 – q3)
Deze winstfunctie kan worden gemaximaliseerd door de afgeleide te bepalen:
dwinst/dq3: 1 – q1 – q2 – 2q3
Dit stellen we gelijk aan 0.
Q3 (SPNE) = (1 – q1 – q2)/ 2
Bedrijf 2:
De vraagfunctie van bedrijf 2 is p = 1 – q1 – q2 – [ (1 – q1 – q2)/2 ]
De winstfunctie van bedrijf 2 is winst = q2 x p oftewel winst = q2 x { 1 – q1 – q2 – [ (1 – q1 – q2)/2 ] }
Deze winstfunctie kan worden gemaximaliseerd door de afgeleide te bepalen:
Dwinst/dq2: (1 – q1) / 2 - q2 (ga dit na! Vereenvoudig eerst de winstfunctie)
Dit wordt vervolgens gelijkgesteld aan 0.
Q2 (SPNE) = (1 – q1) / 2
Bedrijf 1:
De vraagfunctie van bedrijf 1 is p = 1 – q1 – [ (1 –q1)/2 ] - [ (1 – q1 – [(1 –q1)/2] )/2 ]
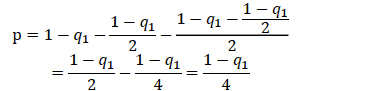
De winstfunctie van bedrijf 1 is winst = q1 x p oftewel winst = q1 x (1 – q1 / 4). Deze winstfunctie kan worden gemaximaliseerd door de afgeleide te bepalen:
Dwinst/dq1: ¼ - 1/2q1
Dit stellen we gelijk aan 0.
Q1 (SPNE) = ½
Eindelijk is de hoeveelheid gevonden dat bedrijf 1 zal produceren, namelijk q1 = ½ .
Nu kunnen ook de ‘output levels’ van de andere twee bedrijven worden bepaald.
q1* = ½
q2* = (1 – 1/2) / 2 = 1/4
q3* = (1 – 1/2 – 1/4)/ 2 = 1/8
De marktprijs zal vervolgens worden P = 1 – ½ - ¼ - 1/8 = 1/8
De winsten voor de bedrijven moeten ook nog worden berekend, let op dat je dat nog niet gedaan hebt! Je hebt m.b.v. de winstfunctie de optimale ‘output levels’ bepaald, maar nog niet letterlijk de winst met dit optimale output level.
Winst bedrijf 1 = P x q1 = 1/8 x ½ = 1/16
Winst bedrijf 2 = P x q2 = 1/8 x ¼ = 1/32
Winst bedrijf 3 = P x q3 = 1/8 x 1/8 = 1/64
Nu het finale antwoord op de vraag, namelijk wat zijn de SPNE? Dit kan je bepalen via de winsten die de bedrijven in de optimale ‘output level’ behalen.
(1/16 , 1/32 , 1/64) is het SPNE

































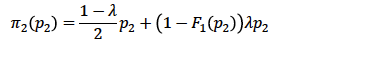







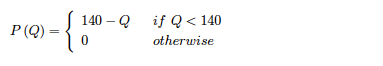

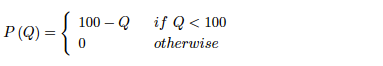
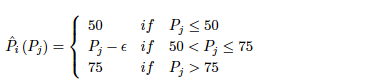
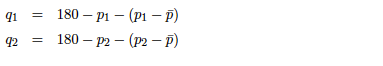

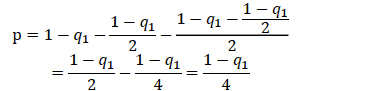







Add new contribution