Psychometrics - IBP Year 2 - Lecture notes
Lecture 1: Measurement, Scaling & Norms
- Psychometrics is the science of measuring mental capacities and processes. In practice, it is the branch of psychology that is concerned with the design, use and evaluation of psychological tests, and the application of statistical mathematical techniques to psychological testing.
- COTAN is the Committee on Tests & Testing of the Dutch Association of Psychologists (NIP). Every once in a while, they evaluate tests based on their theoretical basis, the quality of the test material, quality of the manual, the norms, reliability, construct validity and criterion validity.
- We measure psychological constructs, which are not observable; latent variables, by measuring observable behavior; for which we use operational definitions.
- We aim to observe behavior in a systematic manner; so we use a systematic behavioral sample.We measure observable behavior in order to make statements about the psychological construct, for the purpose of making comparisons between different people (inter-individual differences) and within people (intra-individual differences).
- Researchers deal with the question of how they should give interpretation to their psychological measures; e.g. what if everybody answers ‘yes’ to all the items? What if an individual answers ‘yes’ to 9 out of the 10 items? When drawing conclusions from this information, we should consider biases, review the validity of the test, etc.
- Scaling is the process of assigning definitions to the scores in a test. In the process of scaling, definition refers to the way numerical values are assigned to psychological attributes. So; how is a test score or category determined from the item responses?
- As we’ve encountered last year, there are four scales of measurement: nominal (identity), ordinal (identity + order), interval (identity + order + quantity) and ratio (identity + order + quantity + absolute zero point). Remember that the interval scale requires that there the categories are similar in their width.
- Norming refers to the interpretation of test scores. Relative norming is what we do when we compare a score to relevant other scores. When we compare a score to a fixed standard, it is called absolute norming.
- To obtain a fixed standard, we calculate z. z = (x – μ) ÷ σ. When standardizing our scores, we obtain a mean of 0 and a standard deviation (σ) of 1. When comparing an individual score, we calculate the number of standard deviations it differs from the mean. Z can be a negative value or a positive value.
- In order to interpret a test score, we convert the standard score to T. T = μ × z + σ.
T can only be a positive value.
- To interpret test scores, we can also use percentile ranks: P. It informs us of the percentage of scores that are below or equal to a specific test score.
We convert x --> P by making a table that displays the raw scores in order, with their individual frequency formulated in percentages. We calculate the cumulative frequency of X. Then, we know the x% of the reference sample has the same or a lower score.
- When we have computed an individual’s t-score, z-score or percentile (relative norms), we still have to label this score to interpret the score.
- To interpret one’s score, we use norms. When we do this, we must consider whether the data is still up-to-date, whether the reference sample is of sufficient size and whether the reference sample is representative. We should review the participant’s reactivity and consider social desirability and malingering, we should consider the expectation bias and score sensitivity.
Lecture 2: Reliability
Reliability and validity
- Reliability = to what extent are differences in test scores a function of real individual differences (true scores). So, to what extent is the test free of random errors?
- Validity = to what extent does the test measure what it intends to measure (next week’s topic). So, to what extent is the test free of systematic errors?
Classical test theory (CTT)
- The classical test theory: for every subject, the observed score is the sum of the true score and random error. So, XO (observed score)= Xt(true score) + Xe (error).
- The true score is not directly observable; it is a latent variablethat we can only estimate.
- Error is the difference between the observed score and the true score. It can either be positive or negative. Error is also a latent variable.
- The assumptions of the CTT:
1. μe= 0
The mean error in the population is zero. There is no systematic over- or underestimation of true scores for the population as a whole.
2. ρet= 0
Errors are completely uncorrelated with true scores. There is no systematic over- or underestimation of true scores in subpopulations.
3. reiej = 0
Errors are completely uncorrelated with each other. Error of subject 1 says nothing about the error of subject 2.
- The variance of observed scores is equal to true score variance plus error variance:
s2O = s2t+ s2e.
- A real test is a mixture of the ideal test; in which all observed variance is true score variance; and a completely useless test; in which all observed variance is error variance.
Reliability coefficient
- The reliability coefficient (Rxx) = the proportion of variance of observed scores explained by true scores:
- If the CTT assumptions are valid, then in all cases 0 ≤Rxx≤1.
- The proportion of explained variance is a squared correlation, so therefore an alternative definition of reliability is squared correlation of observed scores with true scores:
- The unsquared correlation rotis called the reliability index.
Estimating reliability: two measurement
- With two or more test scores per subject, making estimates is possible.
- Parallel measurements:
1. Alternate forms (parallel tests): two different tests for the same construct.
2. Test-retest: same test done at two different times.
3. Split-half: two parallel half-tests.
1. Alternate forms:
- Requirement: two measurements (X and Y) must be parallel, which means they measure exactly the same true scores (tau-equivalence). Also, they should have identical error variances.
- Consequences of parallelism:
- Identical observed variances
- Identical correlations with the true score
- Everything that Xo and Yo have in common stems from the shared true score Xt(since errors Xeand Yeare completely uncorrelated.)
- Therefore, the partial correlation between Xo and Yo should be 0.
- And because rxtand ryt are equal; Rxx = Ryy
- The correlation between two parallel tests gives an estimate of the reliability in both tests.
- There are two problems with the alternate forms method:
--> How can we know that the two tests are truly parallel? We can never know, since the true scores are unknown and their variance is estimated under assumption of parallelism.
Partial solutions:
- Domain sampling: Select k items of the two parallel tests randomly from a pool of possible items.
- Consequences of parallelism: If the tests are parallel, they should have equal means and standard deviations.
--> Carry-over effects: taking test 1 can influence the results of test 2 (correlated errors). It can lead to the correlation between the tests being too high; an over-estimation of reliability.
2. Problems with test-retest: people change, which can lead to an underestimation of reliability. Also, carry-over effects play a role, leading to correlated errors (overestimation of reliability) or a change in error variance (over- or underestimation).
3. Split-half: a correlation between (parallel) half-tests. It is an estimation of the reliability of the half-tests.
- The Spearman-Brown formula gives the effect on reliability of lengthening (or shortening) the test: “If test with known reliability (Rxx-original) were made n times as long (with comparable items), what would be the reliability of the lengthened test (Rxx-revised)?”
General version: Rxx-revised= nRxx(original) / 1+(n-1)Rxx(original)
Split-half (n=2): Rxx-total= 2Rxx(subtest) / 1 + Rxx(subtest) = 2rhh / 1 + rhh
n = k(revised) / k(original)
- Problems with split-half:
--> Parallelism: The half-tests must be parallel.
--> Many splits are possible.
Limited solution:
- Most parallel half-test
- Parallel item-pairs
- Evaluation of solution.
Estimating reliability: more than 2 measurements
- Internal consistency is deriving reliability from correlation between parts of tests: 2 measurements: split-half. >2 measurements: treat each item as a separate test --> unique split into k parts.
- Standardized coefficient alpha: Two-step procedure; based on only a number of items (k) and correlation between items (rii).
1. Reliability of each item. This can be estimated by computing the mean correlation between all items. Rii = rbarii
2. Reliability for total test. NB: The estimate of Rxx assumes that we only add up the items after conversion into standard scores!
Rxx = )
- Norms for reliability coefficients:
Important individual-level decisions: r ≥ 0.90 = good, r ≤0.80 = insufficient
Less important individual-level decisions: r ≥0.80 = good, r ≤0.70
Group-level research: r≥0.70 = good, r ≤0.60 = insufficient
Estimating the standard error of measurement and true scores
- When we have estimated Rxx, we can also estimate st2and se2:
st2= so2Rxx se2– so2– so2Rxx = so2(1-Rxx)
- The standard error of measurement sem is standard deviation of error:
sem = se= square root: so2(1-Rxx) = so(square root; 1-Rxx)
- Estimating true scores:
1. Ignoring regression towards the mean
2. Taking regression into account
Assumptions and limitations
- What if the CTT assumptions are violated?
--> Error variances are not the same (but tau is okay): alpha and KR-20 are better estimates of Rxx than parallel methods.
--> No tau-equivalence and error variances are the same. All methods yield an underestimated score of Rxx.
Lecture 3: Validity
- Validity measures to what extent the test measures what it intends to measure. To what extent is the test score free of systematic measurement errors?
- Important points about validity:
> Validity is about the interpretation and use of test scores in relation to certain goals.
> Validity is multidimensional (relates to different goals) and gradual (more-less rather than yes-no)
> Crucial roles of empirical and theoretical support
- The Dutch organisation COTAN evaluates the quality of psychological tests.
- Construct validity refers to what extent test scores can be interpreted as measurements of a certain psychological construct?
1. Test content: Content validity: if a test is intended to measure a certain
construct, items should correspond with the most important sub-constructs of that construct. Example:
- Construct: math ability
- Sub-contstructs: ability in addition, subtraction and multiplication.
- Items: math questions for each of these sub-constructs.
- Threats to content validity are the including of construct-irrelevant content; items that are irrelevant to the sub-construct; or construct-underrepresentation; too few or no items for some sub-constructs.
- The facet method: specify facets, specify levels for each facet and make sure that each possible combination of levels is covered by an appropriate number of items. Content validity can then be summarized in a specification table (shows all levels and the number of items that each of the level covers).
2. Internal test structure: do indicators (items or subtest) for a construct form a coherent whole? If yes, we speak of homogeneity; there is one underlying (latent) dimension. If not, we speak of heterogeneity; there are multiple dimension which may of may not be correlated.
We can empirically test internal test structure by estimating reliability (week 2), principal component analysis or confirmatory factor analysis.
3. Response processes: to what extent is there consistency between the psychological processes that are assumed to be used by respondents and that are actually being used by the respondent. Think of social desirable responding, cheating on a test, and differing measurement scales or changes in responses over time.
4. Associations with other variables
- Convergent validity evidence: association with other measures of the same trait should be substantial. Smaller correlations of a related trait can be used.
- Discriminant validity evidence: association with non-related traits should be small.
- Concurrent validity evidence: association with criterion variables measured at the same time.
- Predictive validity evidence: association with criterion variables in the future.
5. Consequences of testing
- Psychological testing may have adverse or unfair consequences. For example, does a test systematically favor one group of people over another? Also, can we use a test that has low reliability and/or predictive validity to make high-stakes decisions about an individual?
Different perspectives on validity
- Criterion validity: How well does the test predict relevant criteria?
- Inductive approach: increase understanding of the constructs that are measured by a test. The focus is on the associations between test and item scores and a wide-range of other variables.
- Construct-guided test development and validation: a test is valid if the underlying construct truly influences the participant’s responses. The focus is on the association between item and subscale scores.
- Evaluating convergent and discriminant validity can be done by putting everything in a MTMM Matrix: Multi-Trait-Multi-Method Matrix.
- The MTMM allows for assessing the association between measures of the same and different constructs; are they as expected? Also, we assess method effects: The difference between monomethod and heteromethod correlations should not be substantial.
4 types of coefficients: heterotrait - heteromethod, heterotrait - monomethod, monotrait - heteromethod, monotrait – monomethod.
| Monomethod | Heteromethod |
Monotrait | Reliability coefficients | Convergent validity coefficients |
Heterotrait | Convergent validity coefficients (different but related constructs) & discriminant validity coefficients (unrelated constructs) | Convergent validity coefficients (different but related constructs) & discriminant validity coefficients (unrelated constructs |
-
- An indication of a method effect is when the MTMM shows a different order than the following: black-blue-green-red: Meaning that monotrait-heteromethodcorrelations should be higher than heterotrait-heteromethodcorrelations. Monotrait-heteromethodcorrelations should also be higher than heterotrait-monomethodcorrelations.
- Application of predictive validity: A problem is that test scores are often ordinal or interval, but decisions are dichotomous.
The classification problem considers how to assign people to groups on the basis of one or more ordinal (/ interval) variables.
The effects of policy deals with how different cut-off points yield different selection ratios and percentages of successes --> Taylor-Russell tables with a specific base rate show the selection ratio, with the predictive validity; leading to the proportion of successes.
- Factors affecting validity coefficients:
1. True association between constructs (which we are interested in)
2. Measurement error and reliability
True linear association between constructs: rxoyo = rxtyt √RxxRyy
Maximum value of correlation: maxrxoyo = √RxxRyy
Correct for unreliability: rxy-adjusted = rxy-original/√Ryy
3. Restricted range
If the range of scores and/or the criterion variable on the test is limited or restricted, observed correlations may underestimate the true correlation between constructs.
4. Skew and relative proportions
If the distribution of a variable is skewed, the observed correlation may underestimate the true correlation between constructs.
5. Method variance
Considering the MTMM matrix, monomethod correlations are generally higher than heteromethod corelations. Observed scores are mostly a function of an assessment method, and not of the construct we aim to measure.
6. Time
If we have more time between measurement occasions, we see lower correlations between test scores.
7. Predictions of single events vs. multiple events
Human behavior in specific situations is inherently difficult to measure and predict precisely. Summing or averaging over multiple items / situations / time points yield better estimates of targeted construct; higher correlations.
Lecture 4: Principal Component Analysis (PCA)
- Principle Component Analysis (PCA) and Exploratory Factor Analysis (EFA) are similar methods, looking for underlying dimensions.
- We have an unobservable psychological construct that we measure by measuring related observable behaviors.
- We can divide psychological constructs into different sub-scores, which include multiple items. These sub-constructs allow us to draw more reliable conclusions.
Dimensions of a test
- Example: Intelligence tests are all positively correlated, so we refer to a positive manifold. A question that arises is; is there one underlying general intelligence dimension?
- Another example: Personality tests can take on an infinite number of dimensions. There are hundreds of possible questions that we can ask participants. Researchers have come up with five underlying dimensions; the Big Five personality traits: agreeable, open, extraverted, stable and conscientious.
- Investigations of dimensionality consider 1) how many dimensions there are, 2) how these dimensions are related to one another and 3) how we interpret these dimensions.
EFA and PCA
- In contrast to EFA, with PCA we don’t assume that there is an underlying factor influencing the variation in the data. With PCA, we just want to algebraically reduce it to a limited number of components.
- Large differences between PCA and EFA:
-> EFA has an explicit model, in which manifest variables are explained by latent variables.
-> PCA is a theoretical rewriting of variables into components
-> EFA has an explicit model for error, whereas PCA does not. In PCA, errors automatically disappear into higher dimensions.
- In practice, EFA and PCA are quite similar.
- EFA and PCA both aim for data reduction. They reduce a relatively large set of variables to a much smaller set of underlying dimensions (which are called principal components, or factors).
- Both techniques are used confirmatory and exploratory.
PCA: An overview
- PCA can be explained in algebraic and geometric terms.
- PCA consists of communalities; which are about the items, and eigenvalues; which are about the components.
- We need to determine how many dimensions/components are in the data; the extraction of components.
- Rotation.
PCA; algebraically
- A principal component (Fj) is a linear combination of the variable (x1 to xp).
- Fj = a1j Xj + a2jX2 … etc.
- PCA differs a bit from one of the assumptions of the classical test theory (CTT); CTT assumes that all items are parallel. However, in PCA each item can have an individual loading (a). So, PCA is more flexible than CTT.
- The weights aij are chosen in such a way that the first component (Fj) explains as much variance of the variable (x1 to xp) as possible. So, we maximize the first eigenvalue.
- Then, each subsequent component (F2 to Fp) explains as much variance as possible again. Yet, these variances are completely uncorrelated to all earlier components.
PCA geometrically
- Variables determine the direction (the axis) in the p-dimensional space.
- All subjects are displayed as points in this space.
- Components, like variables, are vectors (directions in space). The first component is the direction in which points have a maximum dispersion (long axis of ellipse). The second component is chosen in respect to the first component (short axis of ellipse).
- Initially, PCA calculates just as many components as there are variables (k = p). However, because each subsequent component explains less variance that the previous ones, a relatively small number of components (k < p) is usually enough to explain most of the variance of the variables. This leads to PCA giving us data reduction.
PCA’s communalities
- Variance explained for (VAF) comes in two different ways:
--> Communalities consist of VAF of the observed variables.
--> Eigenvalues consists of variance explained by the components.
- Communalities have a component loading (aij); which indicate the correlation of variable xi with component j.
- The squared component loading (aij2) is the proportion of variance of variable xj that is explained by component j.
- Communality (hi2) is the sum of squared component loadings for variable i. It is the sum of all squared component loadings. (Refer to the book for the exact formula).
PCA’s eigenvalues
- Eigenvalues have a component loading (aij); again, the correlation of variable xi with component j.
- The squared component loading (aij2) is the proportion of variance of variable xj that is explained by component j.
- Eigenvalue (λ) is the sum of squared component loadings for component j.
- Eigenvalue (λ) divided by the number of items (p) yields the proportion of VAF.
PCA’s extraction of components
- Eigenvalue larger than one-criterium:
During extraction of components, we only pick the components (factors) with an eigenvalue larger than 1. If the eigenvalue would be smaller than 1, this component explains less variance that a single variable; so there would be no data reduction.
- Elbow (point of inflection; it is called this way because it looks like an elbow in your graph).
If a clear infection point can be seen in your graph/plot, you should choose the solution with the same number of components as the inflection point. We aren’t always able to spot this point of inflection.
- The rule of best interpretation.
Look at all solutions from 1-factor to eigenvalue larger than 1. Out of these,choose the one that is best interpretable or yields the most practical solution.
PCA: Interpretation of factors and rotation
- We use the component loadings to interpret our factors. This can be done either algebraically or geometrically.
- Rotation facilitates this interpretation. Rotation in itself does not change the number of component or VAF; it only changes the perspective on these values.
Interpretation:
- To interpret the loadings, we can make use of the following rule of thumb: Underline loadings with absolute values above .40 are significant.
- For variables with high loadings on the same component, we first determine what these variables have in common. Then we determine whether what distinguished these variables from variables that do not load on this component.
- Plot variables as vectors in a component space; from the origin point to each point of component loading.
The length of the arrow displays how good a variable is explained by the components. The longer the arrow, the better the variable is explained.
The angle of the arrow displays how high the correlation is between the variables; the higher, the bigger the correlation.
- The idea of rotation is that we have found certain components, but the yielded solution is arbitrary. Through rotation, the eventual solution remains the same, whereas we can get a different perspective on the components.
- We can rotate PCA solutions in an infinite number of ways.
PCA: Methods of rotation
- We have different types of rotations that we can choose from. The two most important ones are VARIMAX AND OBLIMIN.
- VARIMAX (which is orthogonal) chooses new axes in such a way that for each factor the variance of squared factor loading is as high as possible. This logically leads to some factors having very high loadings, and others only having close-to-zero loadings. This method is called simple structure.
- OBLIMIN (which is non-orthogonal or oblique) is the same as VARIMAX, but with OBLIMIN, the rotated components can be correlated. The angle that we see in the graph is not 90 degrees. In practise, oblique rotations are more theoretically attractive. However, the interpretation is more difficult. Also, the solutions are often similar to the uncorrelated correlations.
- Rotations change nothing in regard to the solution in total. The proportion of VAF, the communalities and the relationships between the variables remain the same.
- There is, however, a change in the components and their interpretation.
Lecture 5: Confirmatory Factor Analysis (CFA)
- The difference between Confirmatory Factor Analysis (CFA) and the types of factor analysis that we have discussed last week is, lies in the fact that CFA is used confirmatory.
- In a simple structural model, X is related to Y. εy is variance.
- In a multiple factor model; X is related to multiple Y’s. Multiple εy’s are variance. Structural Equation Modelling (SEM) examines explicit models for (causal) relationships between (> 2) variable.
- SEM can estimate and test relationships between latent variables (e.g. intelligence) and manifest variables (e.g. IQ score). With SES, we can test the relationships in a model, but also the model itself.
- A model is a simplified description, especially mathematical ones, of a system or process, to assist calculations and predictions.
- We should always remember that models are simplified descriptions of the world; so they are not in every case 100% accurate.
- A variable might be measured perfectly if it can be directly observed. However, we often deal with indirect measures of manifest variables. Such measures are influenced by what we want to measure (the true score) and random fluctuations and nuisance factors (e.g. how we want to be perceived). This is referred to as measurement error.
- PCA and EFA are exploratory: We determine empirically how many factors/components and which items load on which factors. All indicators load on all common factors. We assume orthogonality; that there are no correlations between the factors.
CFA is confirmatory: We have explicit models (based on a theory) about a) how many factors, b) correlations between factors, and c) which items load on which factors. In CFA we assume that some loadings are zero; some indicators are specific measurement indicators for certain variables. Also, we assume that there are correlations between the factors.
- Steps in CFA:
1. Model specification; make a model based on a theory or previous research.
- What concept are we measuring? How many dimensions are there? Which items load on which dimension?
- Each path in the model has a model parameter: X1 = λ11F1 + E2
λij is the loading of variable i on factor j.
2. Model identification; decide whether this model can be estimated / tested.
- The number of parameters to be estimated (P) must be smaller than the number of observed variances van covariances (V). The model is testable if and only if df > 0; df = V – P.
--> df < 0; under-identified. There is no unique solution or unique parameter estimates; the model is not testable.
--> df = 0; precisely identified. There is a perfect (but usually unstable) solution (no error); there are unique parameter estimates; yet the model is not testable.
--> df > 0; over-identified. Imperfect solutions (so error); unique parameter estimates, and the model is testable.
- We have to set additional requirements for identification; a scale for each latent variable.
3. Parameter estimation; use data to estimate model coefficients (e.g. factor loadings), under the assumption that the model is correct.
4. Model evaluation; use data and parameter estimates for statistical tests + fit measures, to determine whether the model is defensible.
- Discrepancy function: FML(Σsampe’ Σ^model) = log|Σ^ model| - log|Σsample| + trace(ΣsampleΣ^model-1)-p
- This provides ML estimates of all model parameters and a chi-quare value that can be used to test the exact fit of the model:
χ2 (N-1)FML
- Practical problems with the chi-square test of exact fit
> With a large N, it becomes significant very easily, even when there is only a small divergence between the model and data (a large N is needed in CFA, because otherwise parameter estimates may be unstable).
> The hypothesis of exact fit may not be of interest.
> Therefore, also look at descriptive goodness-of-fit measures; these show the extent to which data agrees with the model:
1) RMSEA (root mean square error of approximation): √ (max(o, χ2 – df) / df(N-1))
Rules of thumb: A value smaller than 0.05 indicates good fit; between .05 and .08 adequate fit, and above .10 poor fit.
2) NFI (normed fit index): Values of > .90 indicate an acceptable fit, and > .95 indicate good fit.
3) CFI (comparative fit index): Values of > .95 indicate acceptable fit, and > .97 indicate good fit.
5. Model re-specification; if the model is not good enough, investigate how it can be improved (and repeat steps 2-4).
We can look at standardized residuals and observe where the big differences occur.
6. Model interpretation; describe the results.
Lecture 6: Item-response Theory (IRT)
- Item-response theory is just another way of looking at the aspects in classical test theory; observed score = true score + measurement error.
- In CTT, we use the sum of item scores. We would almost forget that the individual items have their own characteristics as well.
- CTT’s characteristics are very much dependent upon the sample we have chosen. IRT can partly resolve this problem.
- In IRT, subjects and items are on the same scale. We measure the subject’s ability (θ) in relationship to the item. θ is a latent variable; standardized M=0 and SD = 1.
- In CTT, test scores are on the interval scale. In IRT, the items are dichotomous.
- There are multiple IRT models; the Guttman model, the Rasch model (one-parameter logistic model) and the two-parameter logistic model.
- These models all assume underlying latent traits or abilities and they all explain item responses by person and item characteristics. The models differ in their complexity; the number and type of parameters.
- The Guttman model is a deterministic model (no measurement error; not probabilistic). It assumes that the response of the subject to an item is completely determined by the ability of the subject (θs) and the difficulty of the item (βi).
- To visualize this model, we use an item characteristic curve.
- According to the model, if we know the ability of the subject, we can assume if the person will have this item correct or not.
- The curve has a step function: If one’s ability is lower than the difficulty of the item, he will have it incorrect. If one’s ability is higher than the difficulty of the item, he will have it correct.
- Alternatives for this model are probabilistic models; instead of a step-function, the model will have an S-curve. P (item correct) lies between 0 and 1, but contrary to the Guttman model, it rises smoothly as the ability increases.
- The one-parameter logistic model (1PL), or the Rasch model, assumes that only one item characteristic is relevant; namely the difficulty level (βi).
- The formula: P (Xis = 1|θs, βi) = (e (es - βi)) / (1 + e (θs - βi))
- The two-parameter logistic model (2PL), two item characteristics are relevant: the difficulty level (βi) and the discrimination parameter ai: This is the discriminatory power of the item: It is the extent to which an item distinguished between subjects with low and high abilities. It is also the extent to which an item is representative of an underlying construct.
- The formula: P (Xis = 1|θs, βi, ai) = (e [ai (θs - βi)] ) / (1 + e [ai (θs - βi)]
- Formula of item information for a person with ability θ:
Ii(θ) = ai2 * Pi(θ) * (1- Pi (θ))
- The item information is derivative of item response function. The value increases with a.
- The higher the item discrimination, the higher the (maximum) item information. The item information is highest at item difficulty.
- The sum of item informations: T(θ) Σi Ii(θ)
- Test information in IRT is the equivalent of test reliability in CTT. In IRT, a test’s reliability or measurement precision depends on ability level.
- Applications of IRT in psychology: development and improvement of tests, test equating, item bias (differential item functioning (DIF)), person fit and CAT: computerized adaptive testing.
--> Development and improvement of tests: 1) We can improve items based on item characteristics. We can choose to reformulate items, or decide that some items measure a different construct. 2) We can select test items on the basis of item characteristics. So what range of ability is most informative? What degree of discriminatory power do we use?
--> Test equating: We can use anchor items, so we can compare the same parameters in both groups.
--> Person fit: The IRT model returns a respondent’s estimated theta value. Then we can compute the probability of each of the respondent’s item responses, and thereby the probability of a respondent’s response pattern (called person fit).
--> Computerized adaptive testing: Not all items are administered to each of the respondents. The computer selects an item, the respondent answers it, and the computer scores the answer as right or wrong. The computer re-estimates ability score and precision, and adjust the upcoming questions based on these conclusions.
Lecture 7: Bias
- The validity describes to what extent the test score measures what it aims to measure. In other words; to what extent is the test score free of systematic measurement error?
- These systematic measurement errors are the result of bias.
- In psychometrics, bias denotes a lack of validity (and vice versa). Bias may relate to errors in measurement (systematic distortions in measuring a psychological construct) or in prediction (systematic distortions in associations with other variables).
- Test content, internal test structure and response processes; aspects of construct validity; relate to the items that compose the test. The associations with other variables and the consequences of test are related to the use of the test score.
Types of response biases
1. Acquiescence bias (‘yea-‘ or ‘nay-saying bias): The tendency to systematically agree or disagree with statements. In absence of a response bias, we would expect strong negative correlations between original and reworded items.
2. Extreme and moderate responding
3. Social desirability
4. Malingering: Respondent attempt to fake or exaggerate (psychological) problems.
5. Guessing
Methods to do with response bias
1. Managing the testing context; by assuring anonymity, minimizing fatigue, stress, distraction or frustration or telling respondent that inaccurate responses can be detected.
2. Managing the test content; by writing simple items to reduce respondent fatigue and frustration, or items that are neutral in terms of social desirability, or forced choice items. Scales should be balanced; so they should include positively as well as negatively worded items. Correlations between positively and negatively worded items should be high; otherwise they affect the reliability. We would also see that there is a matter of response bias.
3. Adjust the scoring; by making the scale more balanced through negatively and positively worded items. We can correct for guessing by correcting the test score (CTT). With IRT, we can estimate a different model.
4. Detect response bias with validity scales or tests. The MMPI validity scales or the Balanced Inventory of Desirable Responding are methods. If these tests indicate a response bias in individual cases, we should take this conclusion into account when interpreting their test results. If there is a response bias in entire samples, we should include extra test in statistical and theoretical models.
5. Response bias can also be detected using statistical methods. We will come back to this topic.
- Empirical assessment of test bias is done in two different ways. First, we can assess item characteristics and associations between item scores; referred to as internal structure. In order to do this, we can use CFA, CTT and IRT. We measure item, measurement or construct biases.
Secondly, we can also assess associations between test scores and external variables. In order to do this, we use regression analysis. We measure the predictive or test bias.
- If internal or external associations vary with respect to other variables there is a validity problem, thus; a bias.
- Item bias from the CFA perspective: Construct bias can be examined by using factor analysis. We look at whether there is the same number of factors underlying the items responses across groups; whether there is the same pattern of zero and non-zero loadings across groups; and whether there are the same values of factor loadings across groups. If we detect a difference, there is a bias.
- Item bias from CTT perspective:
1. We calculate test scores for the whole sample
2. Select a high and a low scoring group, e.g. the 25% highest and 25% lowest scores.
3. Assess probability of endorsing an item in the high- and low scoring groups separately for the groups. Note: The probability to endorse an item should be determined by the test score; and not by the grouping variable.
- We see whether there are differences between the proportionate scores of the two groups; the discrimination index. If there is a difference, there is a bias.
- Item bias from IRT perspective:
1. We fit the 2PL model on responses for both groups separately
2. We compare the discrimination and difficulty parameters. If there is no difference in parameters there is no differential item functioning (DIF). If there is a difference in beta (difficulty parameter), there is uniform DIF. If there is a difference in alpha (discrimination parameter); there is non-uniform DIF.
- Now, about predictive bias. We assess associations between test scores and external variables. We can do this by the method of regression analysis. If the association varies with respect to other variables, we speak of a bias.
- To assess how well test score X predicts criterion Y, we use the linear regression prediction equation: Y^ = a + b1X
- To assess bias with respect to variable Z, we include an additional main and interaction effect: Y^ = a + b1X + b2Z + b3XZ
XZ is the interaction between test score X and biasing variable Z. In this course, Z is a single, dichotomous variable.
- If b2 and/or b3 are statistically different, there is predictive bias and we will have to include a biasing variable in the model.
Lecture 8: Classification and Discriminant Analysis (DA)
- Up until now, we have addressed psychometrics dimensionally: meaning that we assigned scores to people on (latent) dimensions (interval).
- The decisions based on these scores are mostly categorical: meaning that we constantly consider to which group we should allocate a person (nominal).
- Classification is the process of allocating individuals to groups or categories.
- The general aim of classification is to predict the categorical dependent variable Y (which distinguishes a k amount of groups from each other) as accurately as possible on the basis of p independent interval variables (X1, X2, et cetera).
- Classification can be one-dimensional (p = 1). In this process, we choose the optimal cut-off point.
- Classification can also be multi-dimensional (p > 2). For this, we use discriminant analysis.
- General procedure:
1. Collect data about X-variables in a sample where Y (classification) is already known.
2. Look for the optimal prediction rule to predict Y rom the X variables as accurately as possible within this sample.
3. Use this prediction rule for new cases for which Y is not yet known.
One dimension
- We look for the optimal cut-off point Xc. However, we should keep in mind that groups are rarely perfectly distinct from each other. We always deal with errors; allocating a person to the wrong group.
- False positives are one type of error; we for example allocate an individual to the depressed group though this person is in reality not depressed at all.
- False negatives are the other type of error. A person who is in fact depressed is allocated to the non-depressed group.
- In the optimal process of allocation, as few false positives and negatives occur as possible. This is partly determined by how we regard the different types of errors.
--> If we perceive both errors to be equally as bad, we minimize the sum of false positives and false negatives to a value that is as small as possible.
--> If we perceive some errors to be worse than others, we can move Xc to the left or right.
Multiple dimensions (DA)
- Techniques that we use for two or more dimensions (interval predictors):
1. p > 2, k = 2. In this situation, we use logistic regression analysis (LRA) or discriminant analysis (DA). With two groups, LRA is usually preferred.
2. p > 2, k > 2. In this situation, we always use discriminant analysis (DA).
- In psychometrics we will discuss DA briefly. LRA and DA in more depth will be discussed in the course of Multivariate Data Analysis.
- In DA, we imagine both individual and group profiles as points in a p-dimensional Euclidian space of variables.
- For each individual, we calculate the distance from all group points (centroids) with the generalised Pythagorean theorem:
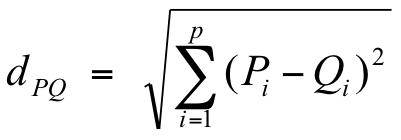
- We then allocate the individual to the group with the shortest distance.
- This is however often not that simple, since some variables have relatively high variances compared to other variables. This means that cut-off lines will move to the group with the smallest variances. Moreover, variables can be correlated, or the data can display non-linear patterns.
- We can end up with multiple possible solutions.
- How good is this solution? We can use a classification table to determine this.
- We calculate the percentage of accuracy in classification (PAC) from this table:
PAC = the number of correct predictions divided by the total number of predictions.
- PAC is however a very rou==gh measure. It is better to have measures based on conditional probabilities; which is the probability of B if H is true.
- These conditional probabilities are important for determining the quality of the measuring instrument and the quality of the individual diagnosis.
- The quality of the measuring instrument is measured by:
--> Sensitivity = number of correctly predicted Depression divided by the total number of Depression.
--> Specificity = number of correctly predicted Non-depression divided by the total number of Non-depression.
- Sensitivity and specificity together determine the quality of the measuring instrument. The ideal measuring instrument misses nobody who is depressed (sensitivity = 1) and does not overestimate anyone who is not depressed (specificity = 1).
- Real measuring instruments in fact make errors. We should also consider the quality of individual diagnoses.
- The quality of individual diagnosis is measured by calculating the probability that an individual actually belongs to the group given a certain diagnosis.
--> Positive predictive value = number of correctly predicted Depression divided by the total number of predicted Depressions.
--> Negative predicted value = number of correctly predicted Non-depressed divided by the total number of predicted Non-depressions.
- With good samples, sensitivity and specificity are independent of the proportions of Depressed and Non-Depressed individuals in the investigated sample.
- The reliability of individual diagnoses is not only determined by the quality of instruments, but also by the base rate in the population. The base rate has no influence on sensitivity and specificity, but it does have an influence on numbers of true and false positives and negatives.
- Sometimes it is better to ignore diagnostic information.
- Bayes’ theorem:
p (A|B) = p(B | A)p(A) / p (B | A)p(A) + p(B|~ A)p(~A)
- The advantages of this theorem are that a connection is made between the ad hoc solution and wider statistical theory. Also, we do not need to know the size of the population because we can work directly with proportions. Lastly, the theorem is generalizable to situations with more than two categories.
Join with a free account for more service, or become a member for full access to exclusives and extra support of WorldSupporter >>

Contributions: posts
Spotlight: topics
JoHo can really use your help! Check out the various student jobs here that match your studies, improve your competencies, strengthen your CV and contribute to a more tolerant world










Add new contribution