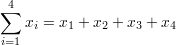Statistics: best definitions, descriptions and lists of terms
 What is statistics?
What is statistics?
Statistics is the science of data, encompassing its collection, analysis, interpretation, and communication to extract knowledge and inform decision-making.
This definition focuses on the core aspects of the field:
- Data-driven: Statistics revolves around analyzing and interpreting data, not just manipulating numbers.
- Knowledge extraction: The goal is to gain insights and understanding from data, not just generate summaries.
- Decision-making: Statistics informs and empowers informed choices in various settings.
Statistics has a wide application:
1. Design and Inference:
- Designing studies: Statisticians use statistical principles to design experiments, surveys, and observational studies that allow for reliable inferences.
- Drawing conclusions: Statistical methods help estimate population parameters from sample data, accounting for uncertainty and variability.
2. Modeling and Analysis:
- Identifying relationships: Statistical models reveal patterns and relationships among variables, aiding in understanding complex systems.
- Quantitative analysis: Various statistical techniques, from regression to machine learning, enable deep analysis of data structures and trends.
3. Interpretation and Communication:
- Meaningful conclusions: Statisticians go beyond numbers to draw meaningful and context-specific conclusions from their analyses.
- Effective communication: Clear and concise communication of findings, including visualizations, is crucial for informing stakeholders and advancing knowledge.
Applications across disciplines:
These core principles of statistics find diverse applications in various academic fields:
- Social sciences: Understanding societal patterns, testing hypotheses about human behavior, and evaluating policy interventions.
- Natural sciences: Analyzing experimental data, modeling physical phenomena, and drawing inferences about natural processes.
- Business and economics: Forecasting market trends, evaluating business strategies, and guiding investment decisions.
- Medicine and public health: Analyzing clinical trials, identifying risk factors for disease, and informing healthcare policies.
Ultimately, statistics plays a crucial role in numerous academic disciplines, serving as a powerful tool for extracting knowledge, informing decisions, and advancing human understanding.
 What is a variable?
What is a variable?
A statistical variable is a characteristic, attribute, or quantity that can assume different values and can be measured or counted within a given population or sample. It's essentially a property that changes across individuals or observations.
Key Points:
- Variability: The defining feature is that the variable takes on different values across units of analysis.
- Measurable: The values must be quantifiable, not just qualitative descriptions.
- Population vs. Sample: Variables can be defined for a whole population or a sampled subset.
Examples:
- Human height in centimeters (continuous variable)
- Eye color (categorical variable with specific options)
- Annual income in dollars (continuous variable)
- Number of siblings (discrete variable with whole number values)
Applications:
- Research: Identifying and measuring variables of interest is crucial in research questions and designing studies.
- Data analysis: Different statistical methods are applied based on the type of variable (continuous, categorical, etc.).
- Modeling: Variables are the building blocks of statistical models that explore relationships and make predictions.
- Summaries and comparisons: We use descriptive statistics like averages, medians, and standard deviations to summarize characteristics of variables.
Types of Variables:
- Quantitative: Measurable on a numerical scale (e.g., height, income, age).
- Qualitative: Described by categories or attributes (e.g., eye color, education level, city).
- Discrete: Takes on distinct, countable values (e.g., number of children, shoe size).
- Continuous: Takes on any value within a range (e.g., weight, temperature, time).
- Dependent: Variable being studied and potentially influenced by other variables.
- Independent: Variable influencing the dependent variable.
Understanding variables is crucial for interpreting data, choosing appropriate statistical methods, and drawing valid conclusions from your analysis.
 What is the difference between the dependent and independent variables?
What is the difference between the dependent and independent variables?
The dependent and independent variables are two crucial concepts in research and statistical analysis. They represent the factors involved in understanding cause-and-effect relationships.
Independent Variable:
- Definition: The variable that is manipulated or controlled by the researcher. It's the cause in a cause-and-effect relationship.
- Applications:
- Experimental design: The researcher changes the independent variable to observe its effect on the dependent variable.
- Observational studies: The researcher measures the independent variable alongside the dependent variable to see if any correlations exist.
- Examples: Dose of medication, study method, temperature in an experiment.
Dependent Variable:
- Definition: The variable that is measured and expected to change in response to the independent variable. It's the effect in a cause-and-effect relationship.
- Applications:
- Measures the outcome or response of interest in a study.
- Affected by changes in the independent variable.
- Examples: Plant growth, test score, patient recovery rate.
Key Differences:
| Feature | Independent Variable | Dependent Variable |
|---|---|---|
| Manipulation | Controlled by researcher | Measured by researcher |
| Role | Cause | Effect |
| Example | Study method | Test score |
Side Notes:
- In some cases, the distinction between independent and dependent variables can be less clear-cut, especially in complex studies or observational settings.
- Sometimes, multiple independent variables may influence a single dependent variable.
- Understanding the relationship between them is crucial for drawing valid conclusions from your research or analysis.
Additional Applications:
- Regression analysis: Independent variables are used to predict the dependent variable.
- Hypotheses testing: We test whether changes in the independent variable cause changes in the dependent variable as predicted by our hypothesis.
- Model building: Both independent and dependent variables are used to build models that explain and predict real-world phenomena.
By understanding the roles of independent and dependent variables, you can effectively design studies, analyze data, and draw meaningful conclusions from your research.
 What is the difference between discrete and continuous variables?
What is the difference between discrete and continuous variables?
Both discrete and continuous variables are used to represent and measure things, but they differ in the way they do so:
Discrete variables:
- Represent countable values
- Have distinct, separate categories with no values in between
- Think of them as individual units you can count
- Examples: Number of people in a room, number of correct answers on a test, grades (A, B, C, etc.), size categories (S, M, L), number of days in a month.
Continuous variables:
- Represent measurable values that can take on an infinite number of values within a range
- Don't have distinct categories and can be divided further and further
- Think of them as measurements along a continuous scale
- Examples: Height, weight, temperature, time, distance, speed, volume.
Here's a table to summarize the key differences:
| Feature | Discrete variable | Continuous variable |
|---|---|---|
| Type of values | Countable | Measurable |
| Categories | Distinct, no values in between | No distinct categories, can be divided further |
| Example | Number of apples | Weight of an apple |
Additional points to consider:
- Discrete variables can sometimes be grouped into ranges: For example, instead of counting individual people, you might group them into age ranges (0-10, 11-20, etc.). However, the underlying nature of the variable remains discrete.
- Continuous variables can be converted to discrete by grouping: For example, you could create discrete categories for temperature (e.g., below freezing, warm, hot). However, this loses information about the actual measurement.
 What is a descriptive research design?
What is a descriptive research design?
In the world of research, a descriptive research design aims to provide a detailed and accurate picture of a population, situation, or phenomenon. Unlike experimental research, which seeks to establish cause-and-effect relationships, descriptive research focuses on observing and recording characteristics or patterns without manipulating variables.
Think of it like taking a snapshot of a particular moment in time. It can answer questions like "what," "where," "when," "how," and "who," but not necessarily "why."
Here are some key features of a descriptive research design:
- No manipulation of variables: The researcher does not actively change anything in the environment they are studying.
- Focus on observation and data collection: The researcher gathers information through various methods, such as surveys, interviews, observations, and document analysis.
- Quantitative or qualitative data: Descriptive research can use both quantitative data (numerical) and qualitative data (descriptive) to paint a comprehensive picture.
- Different types: There are several types of descriptive research, including:
- Cross-sectional studies: Observe a group of people or phenomena at a single point in time.
- Longitudinal studies: Observe a group of people or phenomena over time.
- Case studies: Deeply investigate a single individual, group, or event.
Here are some examples of when a descriptive research design might be useful:
- Understanding the characteristics of a population: For example, studying the demographics of a city or the buying habits of consumers.
- Describing a phenomenon: For example, observing the behavior of animals in their natural habitat or documenting the cultural traditions of a community.
- Evaluating the effectiveness of a program or intervention: For example, studying the impact of a new educational program on student learning.
While descriptive research doesn't necessarily explain why things happen, it provides valuable information that can be used to inform further research, develop interventions, or make informed decisions.
 What is a correlational research design?
What is a correlational research design?
A correlational research design investigates the relationship between two or more variables without directly manipulating them. In other words, it helps us understand how two things might be connected, but it doesn't necessarily prove that one causes the other.
Imagine it like this: you observe that people who sleep more hours tend to score higher on tests. This correlation suggests a link between sleep duration and test scores, but it doesn't prove that getting more sleep causes higher scores. There could be other factors at play, like individual study habits or overall health.
Here are some key characteristics of a correlational research design:
- No manipulation: Researchers observe naturally occurring relationships between variables, unlike experiments where they actively change things.
- Focus on measurement: Both variables are carefully measured using various methods, like surveys, observations, or tests.
- Quantitative data: The analysis mostly relies on numerical data to assess the strength and direction of the relationship.
- Types of correlations: The relationship can be positive (both variables increase or decrease together), negative (one increases while the other decreases), or nonexistent (no clear pattern).
Examples of when a correlational research design is useful:
- Exploring potential links between variables: Studying the relationship between exercise and heart disease, screen time and mental health, or income and educational attainment.
- Developing hypotheses for further research: Observing correlations can trigger further investigations to determine causal relationships through experiments.
- Understanding complex phenomena: When manipulating variables is impractical or unethical, correlations can provide insights into naturally occurring connections.
Limitations of correlational research:
- It cannot establish causation: Just because two things are correlated doesn't mean one causes the other. Alternative explanations or even coincidence can play a role.
- Third-variable problem: Other unmeasured factors might influence both variables, leading to misleading correlations.
While correlational research doesn't provide definitive answers, it's a valuable tool for exploring relationships and informing further research. Always remember to interpret correlations cautiously and consider alternative explanations.
 What is an experimental research design?
What is an experimental research design?
An experimental research design takes the scientific inquiry a step further by testing cause-and-effect relationships between variables. Unlike descriptive research, which observes, and correlational research, which identifies relationships, experiments actively manipulate variables to determine if one truly influences the other.
Think of it like creating a controlled environment where you change one thing (independent variable) to see how it impacts another (dependent variable). This allows you to draw conclusions about cause and effect with more confidence.
Here are some key features of an experimental research design:
- Manipulation of variables: The researcher actively changes the independent variable (the presumed cause) to observe its effect on the dependent variable (the outcome).
- Control groups: Experiments often involve one or more control groups that don't experience the manipulation, providing a baseline for comparison.
- Randomization: Participants are ideally randomly assigned to groups to control for any other factors that might influence the results.
- Quantitative data: The analysis focuses on numerical data to measure and compare the effects of the manipulation.
Here are some types of experimental research designs:
- True experiment: Considered the "gold standard" with a control group, random assignment, and manipulation of variables.
- Quasi-experiment: Similar to a true experiment but lacks random assignment due to practical limitations.
- Pre-test/post-test design: Measures the dependent variable before and after the manipulation, but lacks a control group.
Examples of when an experimental research design is useful:
- Testing the effectiveness of a new drug or treatment: Compare groups receiving the drug with a control group receiving a placebo.
- Examining the impact of an educational intervention: Compare students exposed to the intervention with a similar group not exposed.
- Investigating the effects of environmental factors: Manipulate an environmental variable (e.g., temperature) and observe its impact on plant growth.
While powerful, experimental research also has limitations:
- Artificial environments: May not perfectly reflect real-world conditions.
- Ethical considerations: Manipulating variables may have unintended consequences.
- Cost and time: Can be expensive and time-consuming to conduct.
Despite these limitations, experimental research designs provide the strongest evidence for cause-and-effect relationships, making them crucial for testing hypotheses and advancing scientific knowledge.
 What is a quasi-experimental research design?
What is a quasi-experimental research design?
In the realm of research, a quasi-experimental research design sits between an observational study and a true experiment. While it aims to understand cause-and-effect relationships like a true experiment, it faces certain limitations that prevent it from reaching the same level of control and certainty.
Think of it like trying to cook a dish with similar ingredients to a recipe, but lacking a few key measurements or specific tools. You can still identify some flavor connections, but the results might not be as precise or replicable as following the exact recipe.
Here are the key features of a quasi-experimental research design:
- Manipulation of variables: Similar to a true experiment, the researcher actively changes or influences the independent variable.
- No random assignment: Unlike a true experiment, participants are not randomly assigned to groups. Instead, they are grouped based on pre-existing characteristics or naturally occurring conditions.
- Control groups: Often involve a control group for comparison, but the groups may not be perfectly equivalent due to the lack of randomization.
- More prone to bias: Because of the non-random assignment, factors other than the manipulation might influence the results, making it harder to conclude causation with absolute certainty.
Here are some reasons why researchers might choose a quasi-experimental design:
- Practical limitations: When random assignment is impossible or unethical, such as studying existing groups or programs.
- Ethical considerations: Randomly assigning participants to receive or not receive an intervention might be harmful or unfair.
- Exploratory studies: Can be used to gather preliminary evidence before conducting a more rigorous experiment.
Here are some examples of quasi-experimental designs:
- Pre-test/post-test design with intact groups: Compare groups before and after the intervention, but they weren't randomly formed.
- Non-equivalent control group design: Select a comparison group that already differs from the intervention group in some way.
- Natural experiment: Leverage naturally occurring situations where certain groups experience the intervention while others don't.
Keep in mind:
- Although less conclusive than true experiments, quasi-experimental designs can still provide valuable insights and evidence for cause-and-effect relationships.
- Careful interpretation of results and consideration of potential biases are crucial.
- Sometimes, multiple forms of quasi-experimental evidence combined can create a stronger case for causation.
 What are the seven steps of the research process?
What are the seven steps of the research process?
While the specific steps might differ slightly depending on the research methodology and field, generally, the seven steps of the research process are:
1. Identify and Develop Your Topic:
- Start with a broad area of interest and refine it into a specific research question.
- Consider your personal interests, academic requirements, and potential contributions to the field.
- Conduct preliminary research to get familiar with existing knowledge and identify gaps.
2. Find Background Information:
- Consult scholarly articles, books, encyclopedias, and databases to understand the existing knowledge base on your topic.
- Pay attention to key concepts, theories, and debates within the field.
- Take notes and organize your findings to build a strong foundation for your research.
3. Develop Your Research Design:
- Choose a research design that aligns with your research question and data collection methods (e.g., experiment, survey, case study).
- Determine your sample size, data collection tools, and analysis methods.
- Ensure your research design is ethical and feasible within your resources and timeframe.
4. Collect Data:
- Implement your research design and gather your data using chosen methods (e.g., conducting interviews, running experiments, analyzing documents).
- Be organized, meticulous, and ethical in your data collection process.
- Document your methods and any challenges encountered for transparency and reproducibility.
5. Analyze Your Data:
- Apply appropriate statistical or qualitative analysis methods to interpret your data.
- Identify patterns, trends, and relationships that answer your research question.
- Be aware of potential biases and limitations in your data and analysis.
6. Draw Conclusions and Interpret Findings:
- Based on your analysis, draw conclusions that answer your research question and contribute to the existing knowledge.
- Discuss the implications and significance of your findings for the field.
- Acknowledge limitations and suggest future research directions.
7. Disseminate Your Findings:
- Share your research through written reports, presentations, publications, or conferences.
- Engage with the academic community and participate in discussions to contribute to the advancement of knowledge.
- Ensure responsible authorship and proper citation of sources.
Remember, these steps are a general framework, and you might need to adapt them based on your specific research project.
 What is the difference between descriptive and inferential statistics?
What is the difference between descriptive and inferential statistics?
In the realm of data analysis, both descriptive statistics and inferential statistics play crucial roles, but they serve distinct purposes:
Descriptive Statistics:
- Focus: Describe and summarize the characteristics of a dataset.
- What they tell you: Provide information like central tendencies (mean, median, mode), variability (range, standard deviation), and frequency distributions.
- Examples: Calculating the average age of a group of students, finding the most common hair color in a population sample, visualizing the distribution of income levels.
- Limitations: Only analyze the data you have, cannot make generalizations about larger populations.
Inferential Statistics:
- Focus: Draw conclusions about a population based on a sample.
- What they tell you: Use sample data to estimate population characteristics, test hypotheses, and assess the likelihood of relationships between variables.
- Examples: Testing whether a new teaching method improves student performance, comparing the average heights of two groups of athletes, evaluating the correlation between exercise and heart disease.
- Strengths: Allow you to generalize findings to a broader population, make predictions, and test cause-and-effect relationships.
- Limitations: Reliant on the representativeness of the sample, require careful consideration of potential biases and margins of error.
Here's a table summarizing the key differences:
| Feature | Descriptive Statistics | Inferential Statistics |
|---|---|---|
| Focus | Describe data characteristics | Draw conclusions about populations |
| Information provided | Central tendencies, variability, distributions | Estimates, hypotheses testing, relationships |
| Examples | Average age, most common hair color, income distribution | Testing teaching method effectiveness, comparing athlete heights, exercise-heart disease correlation |
| Limitations | Limited to analyzed data, no generalizations | Reliant on sample representativeness, potential biases and error |
Remember:
- Both types of statistics are valuable tools, and the best choice depends on your research question and data availability.
- Descriptive statistics lay the foundation by understanding the data itself, while inferential statistics allow you to draw broader conclusions and explore possibilities beyond the immediate dataset.
- Always consider the limitations of each type of analysis and interpret the results with caution.
 What is the difference between a parameter and a statistic?
What is the difference between a parameter and a statistic?
In the world of data, where numbers reign supreme, understanding the difference between a parameter and a statistic is crucial. Here's the key difference:
Parameter:
- Represents a characteristic of the entire population you're interested in.
- It's a fixed, unknown value you're trying to estimate.
- Think of it as the true mean, proportion, or other measure of the entire population (like the average height of all humans).
- It's usually denoted by Greek letters (e.g., mu for population mean, sigma for population standard deviation).
Statistic:
- Represents a characteristic of a sample drawn from the population.
- It's a calculated value based on the data you actually have.
- Think of it as an estimate of the true parameter based on a smaller group (like the average height of your classmates).
- It's usually denoted by Roman letters (e.g., x-bar for sample mean, s for sample standard deviation).
Here's an analogy:
- Imagine you want to know the average weight of all elephants on Earth (parameter). You can't weigh every elephant, so you take a sample of 100 elephants and calculate their average weight (statistic). This statistic estimates the true average weight, but it might not be exactly the same due to sampling variability.
Here are some additional key points:
- You can never directly measure a parameter, but you can estimate it using statistics.
- The more representative your sample is of the population, the more likely your statistic is to be close to the true parameter.
- Different statistics can be used to estimate different parameters.
 What is the nominal measurement level?
What is the nominal measurement level?
In the realm of data and research, the nominal measurement level represents the most basic way of classifying data. It focuses on categorization and labeling, without any inherent order or numerical value associated with the categories. Imagine it like sorting socks by color - you're simply grouping them based on a distinct characteristic, not measuring any quantitative aspects.
Here are some key features of the nominal measurement level:
- Categorical data: Values represent categories or labels, not numbers.
- No inherent order: The categories have no specific ranking or hierarchy (e.g., red socks are not "better" than blue socks).
- Limited operations: You can only count the frequency of each category (e.g., how many red socks, how many blue socks).
- Examples: Hair color (blonde, brown, black), blood type (A, B, AB, O), eye color (blue, green, brown), country of origin, shirt size (S, M, L).
Here are some important things to remember about the nominal level:
- You cannot perform mathematical operations like addition, subtraction, or averaging on nominal data.
- Statistical tests used with nominal data focus on comparing frequencies across categories (e.g., chi-square test).
- It's a valuable level for initial categorization and understanding basic relationships between variables.
While it may seem simple, the nominal level plays a crucial role in research by setting the foundation for further analysis and providing insights into basic structures and trends within data. It's like the first step in organizing your closet before you can compare shirt sizes or count the total number of clothes.
 What is the ordinal measurement level?
What is the ordinal measurement level?
In the world of data measurement, the ordinal level takes things a step further than the nominal level. While still focused on categorization, it introduces the concept of order. Think of it like sorting t-shirts based on size - you're not just labeling them (small, medium, large), but you're also arranging them in a specific order based on their size value.
Here are the key features of the ordinal measurement level:
- Categorical data: Similar to nominal level, it represents categories or labels.
- Ordered categories: The categories have a specific rank or sequence (e.g., small < medium < large).
- Limited operations: You can still only count the frequency of each category, but you can also compare and rank them.
- Examples: Educational attainment (high school, bachelor's degree, master's degree), movie rating (1-5 stars), customer satisfaction level (very dissatisfied, somewhat dissatisfied, neutral, somewhat satisfied, very satisfied).
Here are some important points to remember about the ordinal level:
- You cannot perform calculations like adding or subtracting ordinal data because the intervals between categories might not be equal (e.g., the difference between "medium" and "large" t-shirts might not be the same as the difference between "small" and "medium").
- Statistical tests used with ordinal data often focus on comparing ranks or order (e.g., median test, Mann-Whitney U test).
- It provides more information than the nominal level by revealing the relative position of each category within the order.
While still limited in calculations, the ordinal level allows you to understand not only the "what" (categories) but also the "how much" (relative order) within your data. It's like organizing your bookshelf not only by genre but also by publication date.
 What is the interval measurement level?
What is the interval measurement level?
In the world of data analysis, the interval measurement level represents a step towards more precise measurements. It builds upon the strengths of the ordinal level by adding equal intervals between categories. Think of it like measuring temperature on a Celsius scale - you have ordered categories (degrees), but the difference between 20°C and 30°C is the same as the difference between 10°C and 20°C.
Here are the key features of the interval measurement level:
- Quantitative data: Represents numerical values, not just categories.
- Ordered categories: Similar to the ordinal level, categories have a specific rank or sequence.
- Equal intervals: The distance between each category is consistent and measurable (e.g., each degree on a Celsius scale represents the same change in temperature).
- Meaningful zero point: The zero point doesn't necessarily represent an absence of the variable, but it maintains a consistent meaning within the scale (e.g., 0°C doesn't mean "no temperature," but it defines a specific reference point).
- Wider range of operations: You can perform calculations like addition, subtraction, and averaging, but not multiplication or division (due to the arbitrary zero point).
- Examples: Temperature (Celsius or Fahrenheit), time (in seconds, minutes, hours), IQ scores, standardized test scores.
Here are some important points to remember about the interval level:
- While intervals are equal, the ratios between values might not be meaningful (e.g., saying someone with an IQ of 150 is "twice as intelligent" as someone with an IQ of 75 isn't accurate).
- Statistical tests used with interval data often focus on means, standard deviations, and comparisons of differences between groups (e.g., t-tests, ANOVA).
- It provides valuable insights into the magnitude and relative differences between data points, offering a deeper understanding of the underlying phenomenon.
Think of the interval level like taking your t-shirt sorting a step further - you're not just ranking sizes but also measuring the exact difference in centimeters between each size. This allows for more precise analysis and comparisons.
 What is the ratio measurement level?
What is the ratio measurement level?
In the realm of measurement, the ratio level stands as the most precise and informative among its peers. It builds upon the strengths of the interval level by introducing a true zero point, allowing for meaningful comparisons of magnitudes and ratios between values. Imagine measuring distance in meters - not only are the intervals between meters equal, but a zero value on the scale truly represents a complete absence of distance.
Here are the key features of the ratio measurement level:
- Quantitative data: Represents numerical values with clear meanings.
- Ordered categories: Similar to previous levels, categories have a specific rank or sequence.
- Equal intervals: Like the interval level, the distance between each category is consistent and measurable.
- True zero point: The zero point signifies the complete absence of the variable (e.g., zero meters means absolutely no distance, zero seconds means no time passed).
- Widest range of operations: You can perform all mathematical operations (addition, subtraction, multiplication, and division) on ratio data, as the ratios between values have real meaning.
- Examples: Length (meters, centimeters), weight (kilograms, grams), time (seconds with a true zero at the starting point), age (years since birth).
Here are some important points to remember about the ratio level:
- It offers the most precise and informative level of measurement, allowing for comparisons of actual magnitudes and ratios.
- Statistical tests used with ratio data often focus on ratios, proportions, and growth rates (e.g., comparing income levels, analyzing reaction times).
- It's not always possible to achieve a true zero point in every measurement situation, limiting the application of the ratio level in some cases.
Think of the ratio level like having a ruler marked not just with numbers but also with clear and meaningful reference points - you can not only measure the length of an object but also say it's twice as long as another object. This level unlocks the most powerful analysis capabilities.
 Startmagazine: Introduction to Statistics
Startmagazine: Introduction to Statistics
Introduction to Statistics: in short
- Statistics comprises the arithmetic procedures to organize, sum up and interpret information. By means of statistics you can note information in a compact manner.
- The aim of statistics is twofold: 1) organizing and summing up of information, in order to publish research results and 2) answering research questions, which are formed by
 Statistics and research: home bundle
Statistics and research: home bundle
Main content and contributions for statistics and research
- 4504 reads