 Statistics: Magazines for encountering Statistics
Statistics: Magazines for encountering Statistics
Knowledge and assistance for discovering, identifying, recognizing, observing and defining statistics.

Generally, we do not know the value of the standard deviation of the (σ), and we have to estimate it with the standard deviation of the sample population (s). However, if we do know the standard deviation of the population we can use the z-test. The term "Z-test" is often used to refer specifically to the one-sample location test comparing the mean of a set of measurements to a given constant when the sample variance is known
First, a hypothesis is formulated. There are two hypotheses: the null hypothesis and the alternative hypothesis. The null hypothesis means that the independent variable did not have an effect. The hypothesis implies that there is no change or difference. For the null hypothesis the symbol H0 is used. The H refers to hypothesis, and the 0 refers to zero effect. Next, there is the alternative hypothesis (H1) which indicates that there is a change or difference. In the context of an experiment, it indicates that the independent variable (for example a treatment method for depression) did have an effect on the dependent variable (extent of depression). When the null hypothesis for example is that the mean depression score is 30 in the population of depressed people, the alternative hypothesis can be that the mean does not equal 30 (µ ≠ 30). In some cases, the direction of the difference is also specified. For example, if it is expected that the group that received treatment has a higher mean, it applies: H1: µ1 < µ2. It is for example possible to indicate with H1 that the mean is lower than 30 (µ < 30) or higher than 30 (µ > 30). The latter possibility is in this example superfluous, because it is almost impossible that a treatment will cause an increase in the degree of depression. In this case we would say that H1 is a one-tailed, for the estimated value is less than the reference value; in opposition a two-tailed hypothesis is appropriate if the estimated value may be more than or less than the reference value.
The mathematical representations of the null and alternative hypotheses are defined below:
To make a founded decision about the (in)correctness of the null hypothesis, certain criteria have to be used. We use the level of significance or the alfa level (α) as criterion. The alfa level is a limit in the normal distribution that distinguishes between scores with a high chance and scores with a low chance of occurring in the sample, if the hypothesis is true. An alfa of 5% (α = 0.05) implies that there is a 5% chance that the result is found by chance. The alfa level is a chance value that is being used to determine highly unlikely sample results, if the null hypothesis is true.
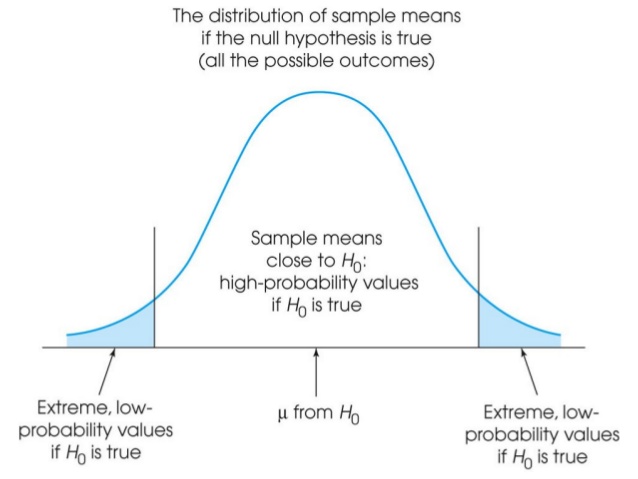
The area that is demarcated with 'extreme low probability values if H0 is true' is called the critical region. The critical region consists of extreme sample values that are highly unlikely if the null hypothesis is true. When a found value falls within this critical region, it differs significantly from the mean and the null hypothesis is rejected. For an alfa of 5%, it implies that 5% of the scores falls within this critical area.
Data are collected after the hypotheses are formulated. This way, the data can be tested by means of the hypothesis; the researcher can evaluate the data in an objective manner. After collecting the raw data, the statistics are calculated. The researcher calculates for example the sample mean. The, the mean can be compared to the null hypothesis. To do so, the researcher has to compute a z-score that describes the position of the sample mean compared to the mean of the null hypothesis. The z-score for the sample mean is calculated:
\[z =\frac{(x - \mu)}{\sigma}\]
The z-score for testing hypotheses is an example of a test statistic.
A researcher uses the z-score from the previous step to make a decision about the null hypothesis. The first possibility is that the researcher rejects the null hypothesis. This is the case when the statistics falls within the critical region. This means that there is a significant difference between the sample and the null hypothesis. The statistic is found in the tail of the distribution. Referring to the example of treating depression, it means that the researcher has found that the treatment had a significant effect. The second possibility is that the null hypothesis can not be rejected. This is the case when the statistic does not fall within the critical area.
As mentioned before: In general, we do not know the value of σ and we have to estimate it with the sample standard deviation (s). When we replace σ by s, we can not use the z-formula, but we have to use the t-test.
\[t =\frac{\bar{x} - \mu}{\frac{s}{\sqrt n}}\]
There are two assumptions that have to be met in order to conduct a t-test.
First, the scores in the sample have to be independent observations. That means that one score can not influence another score. The chance on a certain outcome for a score can thus not be influenced by another score.
Second, the population, from which the sample is drawn, has to be normally distributed. In practice, violation of this assumption has little influence on the t-statistic, especially when the sample size is high. With quite small samples, it is nevertheless important that the population is normally distributed. When you are insecure whether the distribution of the population is normal, it is best to use a high sample size.
The effect size can be computed with Cohen’s d: first the difference between the sample and population mean has to be determined. This has to be divided by the standard deviation of the population. Often, the standard deviation of the population is unknown. Hence, an estimated d is constructed by dividing the difference between sample and population mean by the standard deviation of the sample.
The t-test is used often to test differences between two independent samples. For example, when we compare the achievements between a control group and an experimental group (which received a treatment). We want to examine whether the difference is large enough to assume that the two samples originate from different populations.
When we compare means of two different populations, we test the null hypothesis H0: µ1 - µ2 = 0. This comprises a sampling distribution of all possible difference scores between the population means. In case of two normally distributed populations, the distribution of the difference scores is also normally distributed. The variance of this distribution can be found with the variance sum law: the variance of the sum of the difference of two independent variables equals the sum of there differences:
\[\sigma_{x \pm y}^2 = \sigma_{x}^2 + \sigma_{y}^2\]
So if the variance of set 1 was 2, and the variance of set 2 was 5.6, the variance of the united set would be 2 + 5.6 = 7.6.
The observations in each sample are independent.
The populations from which the samples are drawn, are normally distributed. When the researcher assumes that the populations are not normally distributed, it is advised to use large samples.
The two populations have equal variances. We call this homogeneity of variances. Pooling sampling variance is only useful when both populations have the same variance. This assumption is very important, because a correct interpretation depends upon the research findings. You can check if this assumption is met with Levene’s test in SPSS.
In general, a t-test also assumes that both samples have the same sample size. When the samples do not have an equal sample size, the outcome is biased towards the small sample. To correct for this, a formula is used that combines the variances: the pooled variance. The pooled variance is found by taking the weighted mean of both variances. The sum of squares of both samples is divided by the degrees of freedom. The degrees of freedom are lower for a smaller sample, so that this smaller sample will receive a lower weight. As mentioned before, the variance of a sample (s2) can be obtained by dividing SS by df.
\[s^2 = \frac{SS}{df}\]
To calculate the pooled variance (s2p), a different formula is used:
\[s_{p}^2 = \frac{SS_1 + SS_2}{df_1 + df_2}\]
The estimated standard error of M1-M2 is found by taking the square root of the pooled variance devided by number of cases
\[s_{M_1-M_2} = \sqrt{\frac{s_{p}^2}{n_1 + n_2}}\]
As mentioned before, Cohen’s d can be computed by dividing the difference between the means by the standard deviation of the population. For two independent samples, the difference between the two samples (M1 – M2) is used to estimate the difference in means. The pooled standard deviation (s2p) is used to estimate the standard deviation of the population. The formula to estimate Cohen’s d is thus:
\[Cohen's \: d = \frac{M_1 - M_2}{\sqrt{s_{p}^2}}\]
A paired t-test is used when there is a matched design or when there are repeated measures. The paired t-test takes into account that participants in two conditions are similar to each other. In this case, there are two different samples, but each individual from the one sample is matched to an individual from the other sample. Individuals are matched basis on variables that are considered to be important for the study. This causes an increase of the power: if the independent variable truly has an effect, it is more likely that this will be found in the study. The lower the error variance, the higher the power of the experiment. A high power results in a lower pooled standard deviation (sp). The lower the pooled standard deviation, the higher the t-value.
The t-statistic for related samples is, with regard to its structure, similar to the other t-statistics. The main difference is that the t-statistic for matched samples is based upon difference scores instead of raw scores (X-values). Because participants before and after the treatment are examined, each participant has a difference score. The difference score is:
\[D = X_1 - X_2\]
In this formula, the X2 refers to the second measurement (often: after the treatment). When D is a negative number, it implies that the extent of occurrence of the variable X has decreased after the treatment. A researcher tries to examine whether there is a difference between two conditions in the population by using difference scores. He wants to know what would happen when each individual in the population would be measured twice (before and after the treatment). The researcher strives to know what the mean of the difference score (µD) in the population is.
The null hypothesis is that the mean of the difference scores is zero (H0 : µD = 0). According to this hypothesis, it is possible that some individuals in the population have positive difference scores. In addition, it is possible that some individuals have negative difference scores. However, the main question is whether the mean of all difference scores equals zero. The alternative hypothesis H1 states that the mean of the difference scores does not equal zero (H1 : µD ≠ 0).
The scores within each condition are independent.
The difference scores (D) are normally distributed. Violation of this assumption is not a big matter, as long as the sample sizes are large. For a small sample, this assumption has to be met. A large sample size refers to a sample with at least 30 participants.
If one or more assumptions of the t-test for repeated measures are not met, an alternative test can be used. This is the Wilcoxon-test, in which rank scores are used for comparing difference scores.
The two most frequently used measures for effect size are Cohen’s d and r2 (proportion of explained variance). Because Cohen’s d assumes population parameters (d = µD – σD) it is useful to estimate d. The estimated d can be computed by dividing the mean of the difference scores by the standard deviation (d = MD/s). A value higher than 0.8 is considered a large effect. The proportion of explained variance van be computed as: r2 = t2 / t2 + df.
 Statistics: Magazines for encountering Statistics
Statistics: Magazines for encountering StatisticsKnowledge and assistance for discovering, identifying, recognizing, observing and defining statistics.
 Statistics: Magazines for understanding statistics
Statistics: Magazines for understanding statisticsKnowledge and assistance for classifying, illustrating, interpreting, demonstrating and discussing statistics.
 Statistics: Magazines for applying statistics
Statistics: Magazines for applying statisticsKnowledge and assistance for choosing, modeling, organizing, planning and utilizing statistics.
 Video for what is a t-test?
Video for what is a t-test?T-test made simple
 Video for performing a t-test in practice (by hand)
Video for performing a t-test in practice (by hand)In this video you see how the different mathematical equations are used in order to compare a sample with a population (using a one sample t-test).
In this exercise you will learn how to compare a sample of 20 measures of systolic blood pressure with a known population mean of 120.
Add new contribution